chứng minh rằng nếu ba điểm A,B và C không thẳng hàng thì các điểm A', B' và C' đối xứng với chúng qua điểm O cũng không thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 12 2019
Để ý rằng
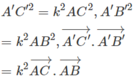
Ta có:
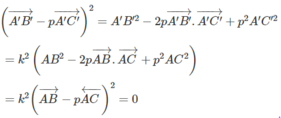
Từ đó suy ra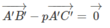 
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó A B → = t A C → , với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A ' B → = t A ' C ' → , với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
13 tháng 9 2015
GIải
Nếu A , B ,C thẳng hàng và A,B,D thẳng hàng
=> 4 điểm A,B,C,D thẳng hàng
Vậy thì B,C,D cũng thẳng hàng
b) Nếu ba điểm A,B,C thẳng hàng và A,B,D không thẳng hàng
=> D không thẳng hàng với A,B,C
Vậy B,C,D cũng không thẳng hàng
2 tháng 7 2023
M đồngthời nằm trong hai góc BAC và góc ABC
=>M nằm trong ΔABC
=>M nằm trong góc BCA
16 tháng 8 2023
THAM KHẢO:
Vì AB và AC cùng vuông góc với một mặt phẳng (P) nên AB trùng AC
⇒⇒ A, B, C thẳng hàng.
A,B,C không thẳng hàng
=>A,B,C là ba đỉnh của ΔABC
=>\(AB+AC>BC;AC+BC>AB;BC+AC>AB\)
Xét tứ giác ABA'B' có
O là trung điểm chung của A'A và BB'
nên ABA'B' là hình bình hành
=>AB=A'B'
Xét tứ giác AC'A'C có
O là trung điểm chung của A'A và C'C
nên AC'A'C là hình bình hành
=>AC=A'C'
Xét tứ giác BC'B'C có
O là trung điểm chung của BB' và CC'
nên BC'B'C là hình bình hành
=>BC=B'C'
\(AB+AC>BC\)
mà AB=A'B' và AC=A'C' và BC=B'C'
nên \(A'B'+A'C'>B'C'\left(1\right)\)
AC+BC>AB
mà AC=A'C' và BC=B'C' và AB=A'B'
nên A'C'+B'C'>A'B'(2)
BA+BC>AC
mà BA=B'A' và BC=B'C' và AC=A'C'
nên B'A'+B'C'>A'C'(3)
Từ (1),(2),(3) suy ra A'B';A'C';B'C' là ba cạnh của một tam giác
=>A',B',C' không thẳng hàng(ĐPCM)