cho hình chóp S.ABCD đáy ABCD là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây
a) AB và CD
b) SA và SC
c) SB và SD
d) SA và BC
e) SD và AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ABCD là hình chữ nhật
=>AD//BC
b: SB cắt SC tại S
=>SB và SC là hai đường thẳng cắt nhau
c: SA cắt SD tại S
=>SA và SD là hai đường thẳng cắt nhau
d: \(SB\subset\left(SBC\right)\)
\(CD\subset\left(SCD\right)\)
Do đó: SB và CD là hai đường thẳng chéo nhau
e: \(SC\subset\left(SBC\right)\)
\(AD\subset\left(SAD\right)\)
Do đó: SC và AD là hai đường thẳng chéo nhau

a: Xét ΔSBD có
H,K lần lượt là trung điểm của SB,SD
=>HK là đường trung bình của ΔSBD
=>HK//BD
mà \(BD\subset\left(ABCD\right)\);HK không thuộc (ABCD)
nên HK//(ABCD)
b: Chọn mp(SBD) có chứa BK
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi E là giao điểm của SO với BK
=>E là giao điểm của BK với mp(SAC)
=>BK cắt (SAC) tại E
c: \(O\in BD\subset\left(SBD\right);S\in\left(SBD\right)\)
Do đó: \(SO\subset\left(SBD\right)\)

a: Xét ΔSAB có H,K lần lượt là trung điểm của SA,SB
=>HK là đường trung bình
=>HK//AB
b: HK//AB
AB//CD
Do đó: HK//CD
c: \(B\in SK\)
\(B\in BC\)
Do đó: SK cắt BC tại B
d: \(HK\subset\left(SAB\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: HK và BC là hai đường thẳng chéo nhau
e: \(HK\subset\left(SAB\right);SD\subset\left(SAD\right)\)
Do đó: HK và SD là hai đường thẳng chéo nhau
f: \(O\in SO\)
\(O\in\left(ABCD\right)\)
Do đó: \(SO\cap\left(ABCD\right)=\left\{O\right\}\)

Chọn đáp án A
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
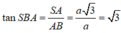
⇒ S B A ⏜ = 60 0

a: Xét ΔSAC có M,N lần lượt là trung điểm của SA,SC
=>MN là đường trung bình của ΔSAC
=>MN//AC
mà MN không thuộc mp(ABCD) và \(AC\subset\left(ABCD\right)\)
nên MN//(ABCD)
b: \(A\in AN;A\in\left(ABD\right)\)
=>\(A\in AN\cap\left(ABD\right)\)
mà \(N\in SC\) không thuộc mp(ABD)
nên \(A=AN\cap\left(ABD\right)\)
c: \(S\in\left(SAC\right);E\in AC\subset\left(SAC\right)\)
Do đó: \(SE\subset\left(SAC\right)\)

Đáp án: D.
Hướng dẫn giải:
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
![]()
S A ⊥ B C ⊥ A M
![]()
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
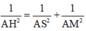
⇒ A H = a 2 5

Đáp án là D
Do SB = SC = 11 và ![]() do đó BC = 11
do đó BC = 11
Ta lại có, SA = SC = 11 và ![]() vuông cân tại S hay AC = 11
2
vuông cân tại S hay AC = 11
2
Mặt khác, SA = SB = 11 và ![]()
Từ đó, ta có ![]() suy ra
∆
ABC vuông tại C
suy ra
∆
ABC vuông tại C
Gọi H là trung điểm của AB Khi đó, H là tâm đường tròn ngoại tiếp ∆ ABC. Vì SA = SB = SC nên SH ⊥ (ABC)
Gọi M là điểm trên CD sao cho HM ⊥ AB suy ra HM ⊥ CD. Gọi N là chân đường vuông góc hạ từ C xuống AB. Khi đó, HM//CN và HM = CN. Do ∆ ABC vuông tại C nên theo công thức tính diện tích ta có:
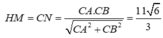
Ta lại có, 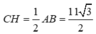 nên
nên ![]()
Trong tam giác vuông SHM dựng đường cao HI(I ∈ SM) suy ra HI ⊥ (SCD). Khi đó,
![]()
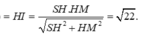
![]()
a: ABCD là hình bình hành
=>AB//CD
b: SA cắt SC tại S
=>SA và SC là hai đường thẳng cắt nhau
c: SB cắt SD tại S
=>SB và SD là hai đường thẳng cắt nhau
d: \(SA\subset\left(SAB\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: SA và BC là hai đường thẳng chéo nhau
d: \(SD\subset\left(SCD\right)\)
\(AB\subset\left(ABCD\right)\)
Do đó: SD và AB là hai đường thẳng chéo nhau