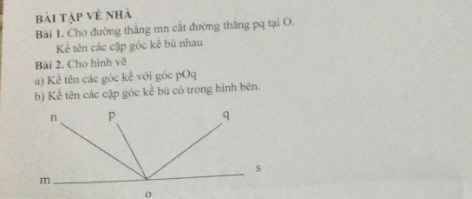
GIẢI GẤP GIÚP T Ạ, T CẦN GẤP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2023
3:
a: \(\sqrt{14^2}=14\)
b: \(\sqrt{16^2}=16\)
c: \(\sqrt{169}=13\)
d: \(\sqrt{\left(\dfrac{3}{4}\right)^2}=\dfrac{3}{4}\)
1:
a: \(\sqrt{144}=\sqrt{12^2}=12\)
b: \(\sqrt{\left(-13\right)^2}=\left|-13\right|=13\)
c: \(-\sqrt{\dfrac{16}{81}}=-\sqrt{\left(\dfrac{4}{9}\right)^2}=-\dfrac{4}{9}\)
d: \(\sqrt{36}+\sqrt{225}=6+15=21\)
HT
giải giúp t ạ t cần gấp giải thì trừ bài 1 ra dùm t ạ
2
12 tháng 5 2023
5:
a: Ngày 1 bán được 45*3/5=27m
b: Ngày 2 bán được 27*1/3=9m
Ngày 3 bán được 27-9=18m
Số mét vải ngày 3 bán được so với ngày 1 là:
18/27=66,66%
GIẢI GẤP GIÚP T Ạ, T CẦN GẤP
30 tháng 8 2023
1:
góc bZc+góc aZb=180 độ(kề bù)
=>góc bZc=180-góc aZb=180-71=109 độ
2: góc pOn+góc pOa=180 độ(kề bù)
=>góc pOa=180-47=133 độ
3: góc xBz+góc xBm=180 độ(hai góc kề bù)
=>góc xBz=180-32=148 độ
20 tháng 5 2022
Part 3: Give the correct form of the verb in brackets. (1,5 m)
Famous places in Ha Noi (visit) ………are visited………every year.
Lan (move) ……………moved…………….to Ho Chi Minh city with her family last summer.
Those students (walk) ………are walking………..up the mountain to visit the shrine of a Vietnamese hero at present.
If we use much pesticide on vegetables, the vegetables (become)………will become……….poisonous and inedible.
How about (make)…………making………….posters on energy and hanging them around our school?
Would you like (have)………to have………..a drink?
Part 4: Give the correct forms of the words in the brackets to finish the following sentences. (1,0 m)
What have fashion designers done to (modern)…………mordernize………the ao dai?
A computer can gather a lot of (inform)…………information…………for different purposes.
In order to keep our environment (pollute) ………unpolluted……….., we shouldn’t drop litter in public places.
Our teacher is pleased that we solved the problems (effect) …………effectively…………..
Part 5: Choose the words or phrases in brackets that best completes each sentence. (1,0 m)
Jeans have never been out of fashion, and today young generation is still fond (in/ on/ at/ of) ……of…….wearing them.
(A/ An/ The/ Every)………The…….Parkers are nice, so van feels like a member of their family.
You (did/ didn’t do/ had/ hadn’t)……didn't do………your homework last night, did you?
If we (go on/ turn off/ look after/ take away)……go on………throwing garbage, the environment will be contamined.
28 tháng 9 2021
Dùng Ca(OH)2 em nha vì khí CO2 và SO2 đều tác dụng được với dd Ca(OH)2
Giải gấp giúp t ạ
H9
HT.Phong (9A5)
CTVHS
15 tháng 8 2023
Hình a:
\(\widehat{zAy}\) và \(\widehat{yAx}\)
Hình b:
\(\widehat{BMA}\) và \(\widehat{AMC}\)
\(\widehat{BAM}\) và \(\widehat{MAC}\)
Hình c:
\(\widehat{pOn}\) và \(\widehat{nOy}\)
\(\widehat{nOy}\) và \(\widehat{yOq}\)
\(\widehat{yOq}\) và \(\widehat{qOm}\)
\(\widehat{qOm}\) và \(\widehat{mOx}\)
\(\widehat{mOx}\) và \(\widehat{xOp}\)
\(\widehat{xOp}\) và \(\widehat{pOn}\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Em xem lại dấu và cách trình bày lúc làm bài nhé.
- Khi mình chia 2 trường hợp mình sẽ dùng dấu [ để biểu thị các trường hợp của biểu thức.
Chẳng hạn như: \(\left[{}\begin{matrix}x+\dfrac{1}{2}=3\\x+\dfrac{1}{2}=-3\end{matrix}\right.\)
Đây là cách trình bày chuẩn nhất nếu em muốn chia 2 trường hợp.
- Còn dấu { để biểu thị các biểu thức phải đồng thời xuất hiện thì mới thỏa mãn biểu thức ban đầu.
Chẳng hạn như: \(x^2+y^2=0\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
Sở dĩ x và y đều phải bằng 0 vì \(x^2\ge0\forall x,y^2\ge0\forall y\) nên trường hợp này dùng dấu {.
Ngoại trừ việc trình bày sai thì đáp số đúng rồi.
CH
26 tháng 9 2023
\(a)\left|x+\dfrac{1}{2}\right|=3\\ x+\dfrac{1}{2}=\left\{{}\begin{matrix}3\\-3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3-\dfrac{1}{2}\\-3-\dfrac{1}{2}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{5}{2}\\-\dfrac{7}{2}\end{matrix}\right.\)
\(b)\left|x-1,5\right|=2\\ x-1,5=\left\{{}\begin{matrix}2\\-2\end{matrix}\right.\\ x=\left\{{}\begin{matrix}2+1,5\\-2+1,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3,5\\-0,5\end{matrix}\right.\\ c)\left|x-2,5\right|-\dfrac{3}{4}=0\\ \left|x-2,5\right|=0+\dfrac{3}{4}\\ \left|x-2,5\right|=\dfrac{3}{4}\\ x-2,5=\left\{{}\begin{matrix}\dfrac{3}{4}\\-\dfrac{3}{4}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{3}{4}+2,5\\-\dfrac{3}{4}+2.5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3,25\\1,75\end{matrix}\right.\)
\(d)\dfrac{1}{2}-\left|\dfrac{5}{4}-2x\right|=\dfrac{1}{3}\\ \left|\dfrac{5}{4}-2x\right|=\dfrac{1}{2}-\dfrac{1}{3}\\ \left|\dfrac{5}{4}-2x\right|=\dfrac{1}{6}\\ \dfrac{5}{4}-2x=\left\{{}\begin{matrix}\dfrac{1}{6}\\-\dfrac{1}{6}\end{matrix}\right.\\ 2x=\left\{{}\begin{matrix}\dfrac{5}{4}-\dfrac{1}{6}\\\dfrac{5}{4}-\left(-\dfrac{1}{6}\right)\end{matrix}\right.\\ 2x=\left\{{}\begin{matrix}\dfrac{13}{12}\\\dfrac{17}{12}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{12}:2\\\dfrac{17}{12}:2\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{24}\\\dfrac{17}{24}\end{matrix}\right.\)
\(e)\left|x-\dfrac{1}{2}\right|=4\\ x-\dfrac{1}{2}=\left\{{}\begin{matrix}4\\-4\end{matrix}\right.\\ x=\left\{{}\begin{matrix}4+\dfrac{1}{2}\\-4+\dfrac{1}{2}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{9}{2}\\-\dfrac{7}{2}\end{matrix}\right.\\ f)\left|x+2,5\right|=3\\ x+2,5=\left\{{}\begin{matrix}3\\-3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}3-2,5\\-3-2,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}0,5\\-5,5\end{matrix}\right.\)
\(g)\left|x+1,5\right|-\dfrac{1}{4}=0\\ \left|x+1,5\right|=0+\dfrac{1}{4}\\ \left|x+1,5\right|=\dfrac{1}{4}\\ x-1,5=\left\{{}\begin{matrix}\dfrac{1}{4}\\-\dfrac{1}{4}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{1}{4}+1,5\\-\dfrac{1}{4}+1,5\end{matrix}\right.\\ x=\left\{{}\begin{matrix}1,75\\1,25\end{matrix}\right.\)
\(h)\dfrac{1}{5}-\left|\dfrac{1}{4}-3x\right|=\dfrac{1}{6}\\ \left|\dfrac{1}{4}-3x\right|=\dfrac{1}{5}-\dfrac{1}{6}\\ \left|\dfrac{1}{4}-3x\right|=\dfrac{1}{30}\\ \dfrac{1}{4}-3x=\left\{{}\begin{matrix}\dfrac{1}{30}\\-\dfrac{1}{30}\end{matrix}\right.\\ 3x=\left\{{}\begin{matrix}\dfrac{1}{4}-\dfrac{1}{30}\\\dfrac{1}{4}-\left(-\dfrac{1}{30}\right)\end{matrix}\right.\\ 3x=\left\{{}\begin{matrix}\dfrac{13}{60}\\\dfrac{17}{60}\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{60}:3\\\dfrac{17}{60}:3\end{matrix}\right.\\ x=\left\{{}\begin{matrix}\dfrac{13}{180}\\\dfrac{17}{180}\end{matrix}\right.\)
H
26 tháng 9 2023
\(a,\left|x\right|+\dfrac{1}{2}=3\\ \Rightarrow\left|x\right|=3-\dfrac{1}{2}\\ \Rightarrow\left|x\right|=\dfrac{5}{2}\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{5}{2}\end{matrix}\right.\)
\(b,10,23-\left|x\right|=5\\ \Rightarrow\left|x\right|=10,23-5\\ \Rightarrow\left|x\right|=5,23\\ \Rightarrow\left[{}\begin{matrix}x=5,23\\x=-5,23\end{matrix}\right.\)
\(c,2\left|x\right|-\dfrac{1}{4}=\dfrac{2}{3}\\ \Rightarrow2\left|x\right|=\dfrac{2}{3}+\dfrac{1}{4}\\ \Rightarrow2\left|x\right|=\dfrac{11}{12}\\ \Rightarrow\left|x\right|=\dfrac{11}{12}:2\\ \Rightarrow\left|x\right|=\dfrac{11}{24}\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{24}\\x=-\dfrac{11}{24}\end{matrix}\right.\)
\(d,6-3\left|x\right|=\dfrac{3}{4}\\ \Rightarrow3\left|x\right|=6-\dfrac{3}{4}\\ \Rightarrow3\left|x\right|=\dfrac{21}{4}\\ \Rightarrow\left|x\right|=\dfrac{21}{4}:3\\ \Rightarrow\left|x\right|=\dfrac{7}{4}\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{4}\\x=-\dfrac{7}{4}\end{matrix}\right.\)
CH
26 tháng 9 2023
\(a)\left|x\right|+\dfrac{1}{2}=3\\ \left|x\right|=3-\dfrac{1}{2}\\ \left|x\right|=\dfrac{5}{2}\\ x=\left\{{}\begin{matrix}\dfrac{5}{2}\\-\dfrac{5}{2}\end{matrix}\right.\\ b)10,23-\left|x\right|=5\\ \left|x\right|=10,23-5\\ \left|x\right|=5,23\\ x=\left\{{}\begin{matrix}5,23\\-5,23\end{matrix}\right.\\ c)2\left|x\right|-\dfrac{1}{4}=\dfrac{2}{3}\\ 2\left|x\right|=\dfrac{2}{3}.\dfrac{1}{4}\\ 2\left|x\right|=\dfrac{11}{12}\\ \left|x\right|=\dfrac{11}{12}:2\\ \left|x\right|=\dfrac{11}{24}\\ x=\left\{{}\begin{matrix}\dfrac{11}{24}\\-\dfrac{11}{24}\end{matrix}\right.\)
\(d)6-3\left|x\right|=\dfrac{3}{4}\\ 3\left|x\right|=6-\dfrac{3}{4}\\ 3\left|x\right|=\dfrac{21}{4}\\ \left|x\right|=\dfrac{7}{4}\\ x=\left\{{}\begin{matrix}\dfrac{7}{4}\\-\dfrac{7}{4}\end{matrix}\right.\)
23 tháng 12 2023
a: Vì \(\widehat{tOn}=\widehat{tOx}\)
và tia Ot nằm giữa hai tia On và Ox
nên Ot là phân giác của góc nOx
b: \(\widehat{mOx}+\widehat{nOx}=180^0\)(hai góc kề bù)
=>\(\widehat{nOx}+50^0=180^0\)
=>\(\widehat{nOx}=130^0\)
Ê, cứu với..
Bài 2:
a) Các góc kề với góc pOq là:
\(\widehat{sOq};\widehat{nOp};\widehat{mOp}\)
b) Các góc kề bù trong hình là:
\(\widehat{mOn}\) và \(\widehat{sOn}\)
\(\widehat{mOp}\) và \(\widehat{sOp}\)
\(\widehat{mOq}\) và \(\widehat{sOq}\)