a) giải thích tại sao AB song song CD
b) tính tổng B^ t C^ ?
K
Khách
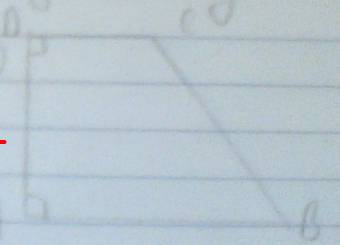
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Vì các thanh chắn của chiếc thang song song với với nhau nên hình chiếu của chúng cũng song song với nhau.
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
23 tháng 8 2017
a) Gọi E, F lần lượt là giao điểm của AM và CD, BN và CD
Ta có : AB//CD (gt) => E = A1 (so le trong)
Mà A1 =A2 (gt)
Nên A2 = E
Xét ΔADE cân tại D, có DM là p/giác nên DM đồng thời là trung tuyến
=>AM= EM
Chứng minh tương tự, ta được :
BN = FN
Xét hình thang ABEF có : AM=BN(cm trên)
BN=FN(cm trên)
Do đó MN là đường TB của HÌNH thang ABEF
=> MN= \(\frac{EF+AB}{2}\)
MN//AB//EF Vậy MN// CD(đpcm)
b)Do ED= AD; BC=FC
Mà ED + DC + CF = EF
Nên AD + DC + BC = EF
Lại có MN \(\frac{EF+AB}{2}\)(CM trên)
Suy ra MN= \(\frac{AD+DC+BC+AB}{2}\)\(=\frac{a+b+c+d}{2}\)
17 tháng 7 2023
a) Xét tứ giác ABCD ta có :
M là trung điểm AD (MA=MD)
M là trung điểm BC (đề bài)
mà (Δ ABC vuông tại A)
⇒ Tứ giác ABCD là hình chữ nhật
⇒ CD song song AB
b) Xét Δ ABE ta có :
BH AE (AH là đường cao)
⇒ BH là đường cao Δ ABE
mà BH là trung tuyến Δ ABE (HE=HA)
⇒ Δ ABE cân tại B
⇒ AB=BE
mà AB=CD (ABCD là hình chữ nhật (cmt))
⇒ CD=BE
c) Ta có : ABCD là hình chữ nhật (cmt)
⇒ CD vuông góc BD
d) Ta có :
AH BC (AH là đường cao) (1)
mà A,H,E thẳng hàng (đề bài)
⇒ AH vuông góc ED (2)
Từ (1) và (2) ⇒ ED song song BC
17 tháng 7 2023
Phần mà Δ ABC vuông tại A ⇒ Góc BAC=90o ⇒ ABCD là hình chữ nhật ( M là trung điểm 2 đường chéo AD và BC và có 1 góc vuông)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_1}}\) (2 góc đồng vị), mà \(\widehat {{A_1}} = 90^\circ \) nên \(\widehat {{B_1}} = 90^\circ \).
Vậy c vuông góc với b.
a) Ta có:
\(CD\perp AD\)
\(AB\perp AD\)
\(\Rightarrow CD//AB\)
b) Ta có:
\(AB//CD\)
Nên: \(\widehat{B}+\widehat{C}=180^o\)
Do hai góc này ở vị trí trong cùng phía