1 hình nón có chiều cao là 3m và mặt cắt qua trục là 1 tam giác đều ,1 hình trụ cũng có chiều cao là 3m và thể tích = thể tích của 1 hình nón .Tính bán kính của hình trụ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AH
Akai Haruma
Giáo viên
26 tháng 5 2022
Lời giải:
Gọi độ dài cạnh tam gaics đều là $a$ thì $a$ chính là đường kính đáy hình nón.
Chiều cao (áp dụng định lý Pitago): $\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}}{2}a$
Theo bài ra:
$\frac{\sqrt{3}}{2}a=12\Rightarrow a=8\sqrt{3}$ (cm)
Bán kính đáy: $a:2=4\sqrt{3}$ (cm)
Diện tích mặt đáy: $\pi R^2=(4\sqrt{3})^2\pi =48\pi$ (cm2)
Thể tích: $\frac{1}{3}.48\pi.12=192\pi$ (cm3)

CM
18 tháng 3 2018
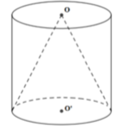
Đáp án B
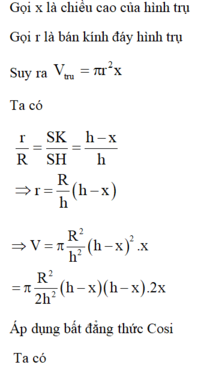
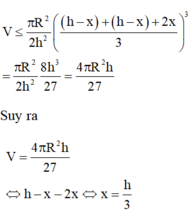
Vậy khi vị trí mặt phẳng α cách đáy hình nón một khoảng h 3 thì khối trụ có diện tích lớn nhất

CM
8 tháng 5 2019
Chọn C.
Phương pháp:
Sử dụng các công thức tính thể tích:

Nhận xét: Hai khối nón và khối trụ có cùng chiều cao h và cùng bán kính đáy bằng r.
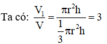
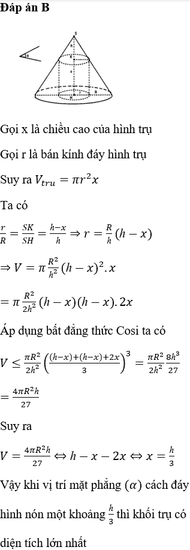
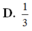

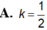
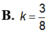
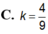
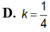

giúp mk bài này vs ạ