Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi độ dài cạnh tam gaics đều là $a$ thì $a$ chính là đường kính đáy hình nón.
Chiều cao (áp dụng định lý Pitago): $\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}}{2}a$
Theo bài ra:
$\frac{\sqrt{3}}{2}a=12\Rightarrow a=8\sqrt{3}$ (cm)
Bán kính đáy: $a:2=4\sqrt{3}$ (cm)
Diện tích mặt đáy: $\pi R^2=(4\sqrt{3})^2\pi =48\pi$ (cm2)
Thể tích: $\frac{1}{3}.48\pi.12=192\pi$ (cm3)

a, Tính được r = 1,44cm Þ Smc = 4p r 2 = 26,03 c m 2
b, Ta có V c = 4 3 πR 2 = 15 , 8 cm 3 => R = 1,56cm
=> V h n = 1 3 πR 2 h ≈ 2 , 53 πcm 3

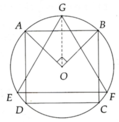
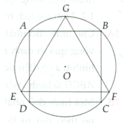
a, V h t A B C D = π AB 2 2 . BC = π AB 3 4 = π 2 2 . R 3 (1)
V h c = 4 3 πR 3 (2)
V h n = 1 3 π EF 2 2 . GH = 1 8 3 π . EF 3 . Tính được GO = 3 R
=> V h n = 1 8 3 π 3 3 R 3 = 3 8 πR 3 (3)
Từ (1), (2) và (3) => ĐPCM
b, S t p h t = 3 πR 2 (4); S h c = 4 πR 2 (5)
S t p h n = 3 4 πEF 2 = 3 4 π . 3 R 2 = 9 4 πR 2 (6)
Từ (4); (5) và (6) => ĐPCM

Thể tích của hình trụ là: π m 2 k
Thể tích của hình nón là: 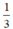 π
m
2
k
π
m
2
k
Vậy thể tích của hình nón bằng 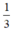 thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là
thể tích hình trụ. Do đó, khi chứa đầy cát vào hình nón rồi đổ hết sang hình trụ thì độ cao của cát trong hình trụ sẽ là 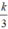

giúp mk bài này vs ạ