Cho tứ giác ABCD có B=D=90 độ.Vẽ phân giác góc A và C biết 2 phân giác này không trùng nhau.CM 2 phân giác đó song song với nhau
Lm nhanh mik tick
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 10 2023
TH1: ABCD không phải là hình thoi hoặc hình vuông
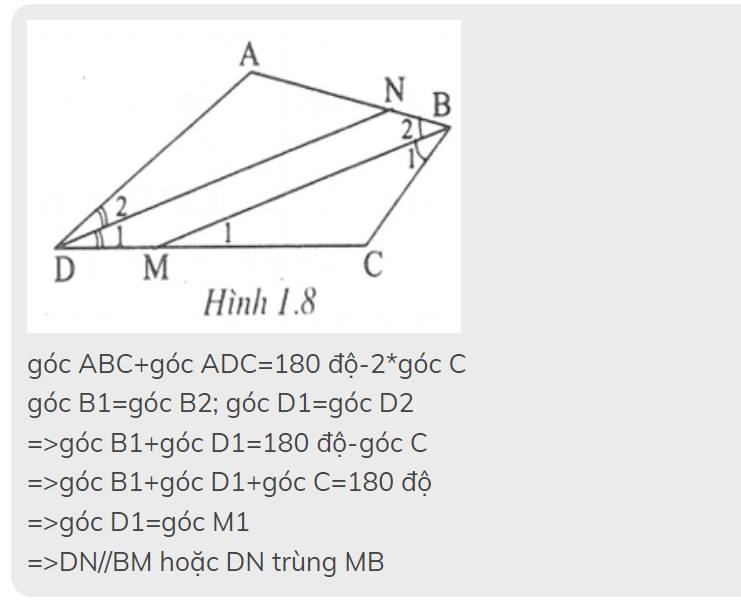
Gọi BM,DN lần lượt là phân giác của \(\widehat{ABC};\widehat{ADC}\)
Xét tứ giác ABCD có
\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(2\cdot\left(\widehat{NBM}+\widehat{NDM}\right)=360^0-\widehat{A}-\widehat{C}=360^0-2\cdot\widehat{C}\)
=>\(\widehat{NBM}+\widehat{NDM}=180^0-\widehat{C}\)(1)
Xét ΔCMB có
\(\widehat{C}+\widehat{CMB}+\widehat{CBM}=180^0\)
=>\(\widehat{CMB}+\widehat{NBM}=180^0-\widehat{C}\)(2)
Từ (1) và (2) suy ra \(\widehat{NDM}=\widehat{CMB}\)
mà hai góc này ở vị trí đồng vị
nên BM//DN (ĐPCM)
TH2: ABCD là hình thoi hoặc hình vuông
ABCD là hình thoi
=>BD là tia phân giác của \(\widehat{ABC}\) và DB là tia phân giác của \(\widehat{ADC}\)
=>Các đường phân giác của góc B và góc D trùng nhau
18 tháng 7
Ta có:
+, Gọi giao của DC và BE là K
Vì DF//BE nên gócCDF =góc CKB ( 2 góc đồng vị )
mà góc CKB +gócCBK =900 ( vì gócC=900 ) ( 1)
+, gócCBK =gócABE ( vì BE là tia pg của gócB)
và gócABE =gócAFD ( vì BE//DF)
=> gócCBK= gócAFD (2)
mà gócAFD +gócADF=900 (vì góc A=900) (3)
Từ (1)(2)(3) ta có góc ADF = góc CDF
=> DF là tia pg của góc D ( đpcm )
Cho mik 1 like nhé!!! Chúc bạn làm bài tốt .
Gọi AE là phân giác góc A( E thuộc CD), CF là phân giác góc C ( F thuộc AB )
H là giao điểm của DA và CF.
Xét \(\Delta DHC\)và \(\Delta BCF\)có:
\(\widehat{B}=\widehat{D}=90^o\)
\(\widehat{DCH}=\widehat{BCF}\left(gt\right)\)
Suy ra \(\Delta DHC\)đồng dạng với \(\Delta BCF\)(g.g)
\(\Rightarrow\widehat{DHC}=\widehat{BFC}\)
Mà \(\widehat{AFH}=\widehat{BFC}\)(ĐỐI ĐỈNH)
nên \(\widehat{AFH}=\widehat{DHC}\)hay \(\widehat{AFH}=\widehat{AHF}\)
Ta có:
\(\widehat{DAF}\)là góc ngoài của \(\Delta AHF\)
\(\Rightarrow\widehat{DAF}=\widehat{AHF}+\widehat{AFH}\)
\(\Leftrightarrow2.\widehat{AFH}=\widehat{DAF}\)
\(\Leftrightarrow\widehat{AFH}=\widehat{\frac{DAF}{2}=\widehat{BAE}}\)
Mà \(\widehat{AFH}=\widehat{BFC}\)(ĐỐI ĐỈNH) nên \(\widehat{BAE}=\widehat{BFC}\)
\(\Rightarrow AE\)//\(CF\)(Vì có hai góc so le trong bằng nhau)
Vậy AE//CF