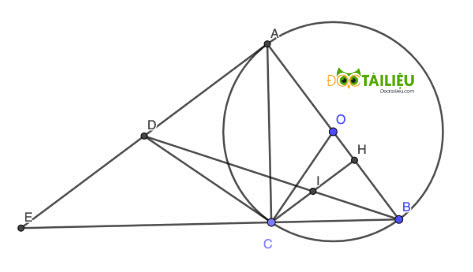
Cho đường tròn tâm O có đường kính AB,D là một điểm nằm trên đường tròn.Các tiếp nhất của đường tròn tại A và D cắt nhau tại C.Gọi E là hình chiếu của D trên AB,gọi I là giao điểm của BC và DE.Chứng minh rằng DI=DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2023
DA,DC là tiếp tuyến của (O)
=>DA=DC
=>OD vuông góc AC
CH vuông góc AB
=>AD//CH
=>CI/AD=IM/MD
IH/AD=BI/BD
mà IM/MD=BI/BD
nên CI/AD=IH/AD
=>CI=IH
3 tháng 7 2023
a: góc AMB=góc AEB=1/2*sđ cung AB=90 độ
Xét ΔBMS vuông tại M và ΔBED vuông tại E có
góc MBS=góc EBD
=>ΔBMS đồng dạng với ΔBED
=>góc BSM=góc BDE
=>góc MSE=góc MDE
=>MSDE nội tiếp
b: Xét ΔSME và ΔSBA có
góc S chung
góc SEM=góc SAB
=>ΔSME đồng dạng với ΔSBA
20 tháng 6 2023
a: góc HCB+góc HEB=180 độ
=>HCBE nội tiếp
Xét ΔACH vuông tại C và ΔAEB vuông tại E có
góc CAH chung
=>ΔACH đồng dạng với ΔAEB
=>AC/AE=AH/AB
=>AC*AB=AE*AH
b: góc IDH=1/2*sđ cung DB
góc IHD=90 độ-góc AMH=1/2*sđ cung DB
=>góc IDH=góc IHD
=>ΔIHD cân tại I
5 tháng 7 2021
DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp
8 tháng 12 2023
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
=>BC\(\perp\)AC tại C
=>BC\(\perp\)AE tại C
=>ΔCEF vuông tại C
Xét (O) có
\(\widehat{ICB}\) là góc tạo bởi tiếp tuyến CI và dây cung CB
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
Do đó: \(\widehat{ICB}=\widehat{CAB}\)
mà \(\widehat{CAB}=\widehat{BFD}\left(=90^0-\widehat{CBA}\right)\)
nên \(\widehat{ICB}=\widehat{BFD}\)
mà \(\widehat{BFD}=\widehat{IFC}\)(hai góc đối đỉnh)
nên \(\widehat{ICB}=\widehat{IFC}\)
=>\(\widehat{ICF}=\widehat{IFC}\)
=>IC=IF
Ta có: \(\widehat{ICF}+\widehat{ICE}=\widehat{ECF}=90^0\)
\(\widehat{IFC}+\widehat{IEC}=90^0\)(ΔECF vuông tại C)
mà \(\widehat{ICF}=\widehat{IFC}\)
nên \(\widehat{ICE}=\widehat{IEC}\)
=>IC=IE
mà IC=IF
nên IE=IF
=>I là trung điểm của EF
b: Vì ΔCEF vuông tại C
nên ΔCEF nội tiếp đường tròn đường kính EF
=>ΔCEF nội tiếp (I)
Xét (I) có
IC là bán kính
OC\(\perp\)CI tại C
Do đó: OC là tiếp tuyến của (I)