Câu 1. Người ta kéo một vật có khối lượng 3 kg lên cao không vận tốc đầu theo phương thẳng đứng. Biết trong 1 s đầu vật đi được quãng đường 0,5 m và sợi dây chịu được sức căng tối đa là 40 N. Lấy g = 9,8 m/s2. Tính độ lớn của lực căng sợi dây và chứng minh sợi dây không bị đứt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu dây cáp chịu được lực căng tối đa T m a x = 6000 N > 4920 N, thì ở cùng độ cao nêu trên vật có thể đạt được vận tốc tối đa v m a x sao cho :
m v m a x 2 /2 + mgh = T m a x h
![]()

Vật nặng chịu lực căng T → (ngoại lực) tác dụng, chuyển động từ mặt đất lên tới độ cao h = 10 m và đạt được vận tốc v = 0,5 m. Trong trường hợp này, độ biến thiên cơ năng của vật có giá trị bằng công do ngoại lực thực hiện, nên ta có :
m v 2 /2 + mgh = Th
suy ra lực căng của sợi dây cáp :
T = m( v 2 /2h + g) ≈ 500(4,5. 0 , 6 2 /2 + 9,8) = 4920(N)

Độ biến dạng tại vị trí cân bằng của dây là

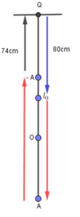
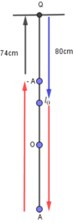
Chia dao động của vật làm 3 giai đoạn được biểu diễn như hình vẽ
Đáp án B

Đáp án B
Độ biến dạng tại vị trí cân bằng của dây là

Chia dao động của vật làm 3 giai đoạn được biểu diễn như hình vẽ

a)Cơ năng vật:
\(W=W_đ+W_t=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot0,5\cdot25^2+0,5\cdot10\cdot0=156,25J\)Độ cao cực đại:
\(W=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{156,25}{0,5\cdot10}=31,25m\)
b)Để \(W_t=W_đ\Rightarrow mgz=\dfrac{1}{2}mv^2\)
\(\Rightarrow z=\dfrac{v^2}{2g}=\dfrac{25^2}{2\cdot10}=31,25m\)

a) Độ cao cực đại mà vật đạt được :
\(h_{max}=\dfrac{W}{0,5.10}=31,25\left(m\right)\)
b) \(W_t=W_đ\Rightarrow mgz=\dfrac{1}{2}mv^2\Rightarrow z=\dfrac{v^2}{2g}=\dfrac{25^2}{2.10}=31,25\left(m\right)\)
c) Vận tốc mà thế năng bằng 3 lần động năng :
Khi thế năng bằng 3 lần động năng
\(\Rightarrow\dfrac{1}{3}W_t=W_đ\)
\(\Rightarrow\dfrac{1}{3}.mgz=\dfrac{1}{2}mv^2\)
\(\Rightarrow mv^2=\dfrac{2}{3}mgz\)
Làm tiếp :
\(\Rightarrow mv^2=\dfrac{2}{3}.0,5.10.31,25=\dfrac{625}{6}\)
\(\Rightarrow v^2=\dfrac{625}{6}.2=\dfrac{625}{3}\)
\(\Rightarrow v=\sqrt{\dfrac{625}{3}}=\dfrac{25\sqrt{3}}{3}\approx14,4338\left(\dfrac{m}{s}\right)\)