x mũ 3 : (-1/2 mũ 2) = 1/2 cứu tui với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
3
LN
Lưu Nguyễn Hà An
CTVHS
14 tháng 1 2024
Ta có : 2^x+2^{x+1}+2^{x+2}+...+2^{x+2015}=2^{2019}-82x+2x+1+2x+2+...+2x+2015=22019−8
\Leftrightarrow2^x\left(1+2+2^2+...+2^{2015}\right)=2^{2019}-8⇔2x(1+2+22+...+22015)=22019−8 (1)
Đặt : A=1+2+2^2+...+2^{2015}A=1+2+22+...+22015
\Rightarrow2A=2+2^2+2^3+...+2^{2016}⇒2A=2+22+23+...+22016
\Rightarrow2A-A=\left(2+2^2+2^3+...+2^{2016}\right)-\left(1+2+2^2+...+2^{2015}\right)⇒2A−A=(2+22+23+...+22016)−(1+2+22+...+22015)
\Rightarrow A=2^{2016}-1⇒A=22016−1
Khi đó (1) trở thành :
2^x\left(2^{2016}-1\right)=2^{2019}-2^32x(22016−1)=22019−23
\Leftrightarrow2^x\left(2^{2016}-1\right)=2^3\left(2^{2016}-1\right)⇔2x(22016−1)=23(22016−1)
\Leftrightarrow2^x=2^3\left(2^{2016}-1\ne0\right)⇔2x=23(22016−1=0)
\Leftrightarrow x=3⇔x=3
Vậy : x=3x=3
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 1 2024
2x+2x+1+...+2x+2015=22019−82�+2�+1+...+2�+2015=22019-8
→2x.1+2x.2+....+2x.22015=22019−8→2�.1+2�.2+....+2�.22015=22019-8
→2x.(1+2+...+22015)=22019−8→2�.(1+2+...+22015)=22019-8
Đặt:
A=1+2+...+22015�=1+2+...+22015
2A=2.(1+2+...+22015)2�=2.(1+2+...+22015)
2A=2+22+...+220162�=2+22+...+22016
2A−A=(2+22+...+22016)−(1+2+...+22015)2�-�=(2+22+...+22016)-(1+2+...+22015)
A=2+22+...+22016−1−2−...−22015�=2+22+...+22016-1-2-...-22015
A=22016−1�=22016-1
Nên:
2x.(1+2+...+22015)=22019−82�.(1+2+...+22015)=22019-8
→2x.(22016−1)=22019−8→2�.(22016-1)=22019-8
→2x=(22019−8):(22016−1)→2�=(22019-8):(22016-1)
→2x=22019−822016−1→2�=22019-822016-1
→2x=23.(22016−1)22016−1→2�=23.(22016-1)22016-1
→2x=23→2�=23
→x=3→�=3
Vậy x=3.
T
8 tháng 11 2023
\(B=2^2+2^3+2^4+...+2^{121}\\=(2^2+2^3)+(2^4+2^5)+(2^6+2^7)+...+(2^{120}+2^{121})\\=2^2\cdot(1+2)+2^4\cdot(1+2)+2^6\cdot(1+2)+...+2^{120}\cdot(1+2)\\=2^2\cdot3+2^4\cdot3+2^6\cdot3+...+2^{120}\cdot3\\=3\cdot(2^2+2^4+2^6+...+2^{120})\)
Vì \(3\cdot(2^2+2^4+2^6+...+2^{120})\vdots3\)
nên \(B\vdots3\)
T
22 tháng 12 2023
\(A=2^0+2^1+2^2+2^3+2^4+2^5+\dots+2^{100}\\=(2^1+2^2)+(2^3+2^4)+(2^5+2^6)+\dots+(2^{99}+2^{100})+2^0\\=2\cdot(1+2)+2^3\cdot(1+2)+2^5\cdot(1+2)+\dots+2^{99}\cdot(1+2)+1\\=2\cdot3+2^3\cdot3+2^5\cdot3+\dots+2^{99}\cdot3+1\\=3\cdot(2+2^3+2^5+\dots+2^{99})+1\)
Vì \(3\cdot(2+2^3+2^5+\dots+2^{99})\vdots3\)
\(\Rightarrow 3\cdot(2+2^3+2^5+\dots+2^{99})+1\) chia \(3\) dư 1
hay số dư của phép chia \(A\) cho \(3\) là \(1\).
22 tháng 12 2023
A=2^0 + 2^1 + 2^2 + 2^3 + 2^4 + ....+2^100
A=1 + 2^1 + 2^2 + 2^3 + 2^4 + ....+2^100
A=1 + (2^1 + 2^2) + (2^3 + 2^4) + ....+(2^99 + 2^100)
A=1 + 2.(1+2) + 2^3.(1+2)+....+2^99.(1+2)
A=1 + 2 . 3 + 2^3 . 3 +....+2^99 . 3
A=1 +3 .(2+2^3+..+2^99)
=> A:3 dư 1
13 tháng 5 2018
a)<=>
A,=(x+y)(x-y)=x^2-y^2
x=(-1/2)^5:(1/2)^4=-1/2
x^2=1/4
y=8^2/(-2)^5=-2
y^2=4
A=1/4-4=-15/4
G
8 tháng 9 2020
a) \(1,25^2-0,5^2+3,25^3\)
\(=\left(\frac{5}{4}\right)^2-\left(\frac{1}{2}\right)^2+\left(\frac{13}{4}\right)^3\)
\(=\frac{25}{16}-\frac{1}{4}+\frac{2197}{64}\)
\(=\frac{2281}{64}\)
b) \(1,2+2,4^2-\left(3\frac{1}{2}\right)^2\)
\(=\frac{6}{5}+\left(\frac{12}{5}\right)^2-\left(\frac{7}{2}\right)^2\)
\(=\frac{6}{5}+\frac{144}{25}-\frac{49}{4}\)
\(=\frac{-529}{100}\)
24 tháng 10 2023
`(2^x+1)^2 =25`
`=> (2^x+1)^2 = (+-5)^2`
\(\Rightarrow\left[{}\begin{matrix}2^x+1=5\\2^x+1=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2^x=4\\2^x=-6\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x\in\varnothing\end{matrix}\right.\)
\(\left(x+6\right)\left(5^x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+6=0\\5^x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\5^x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=0\end{matrix}\right.\)
\(\left(x-3\right)^{2023}=x-3\)
\(\Rightarrow\left(x-3\right)^{2023}-\left(x-3\right)=0\)
\(\Rightarrow\left(x-3\right)\left[\left(x-3\right)^{2022}-1\right]=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\\left(x-3\right)^{2022}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\\left(x-3\right)^{2022}=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x-3=1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=4\end{matrix}\right.\)
DN
1
29 tháng 7 2021
Thay \(x=\dfrac{1}{2}\) vào A, ta được:
\(A=3\cdot\left(\dfrac{1}{2}\right)^2-2\cdot\dfrac{1}{2}+1=\dfrac{3}{4}-1+1=\dfrac{3}{4}\)
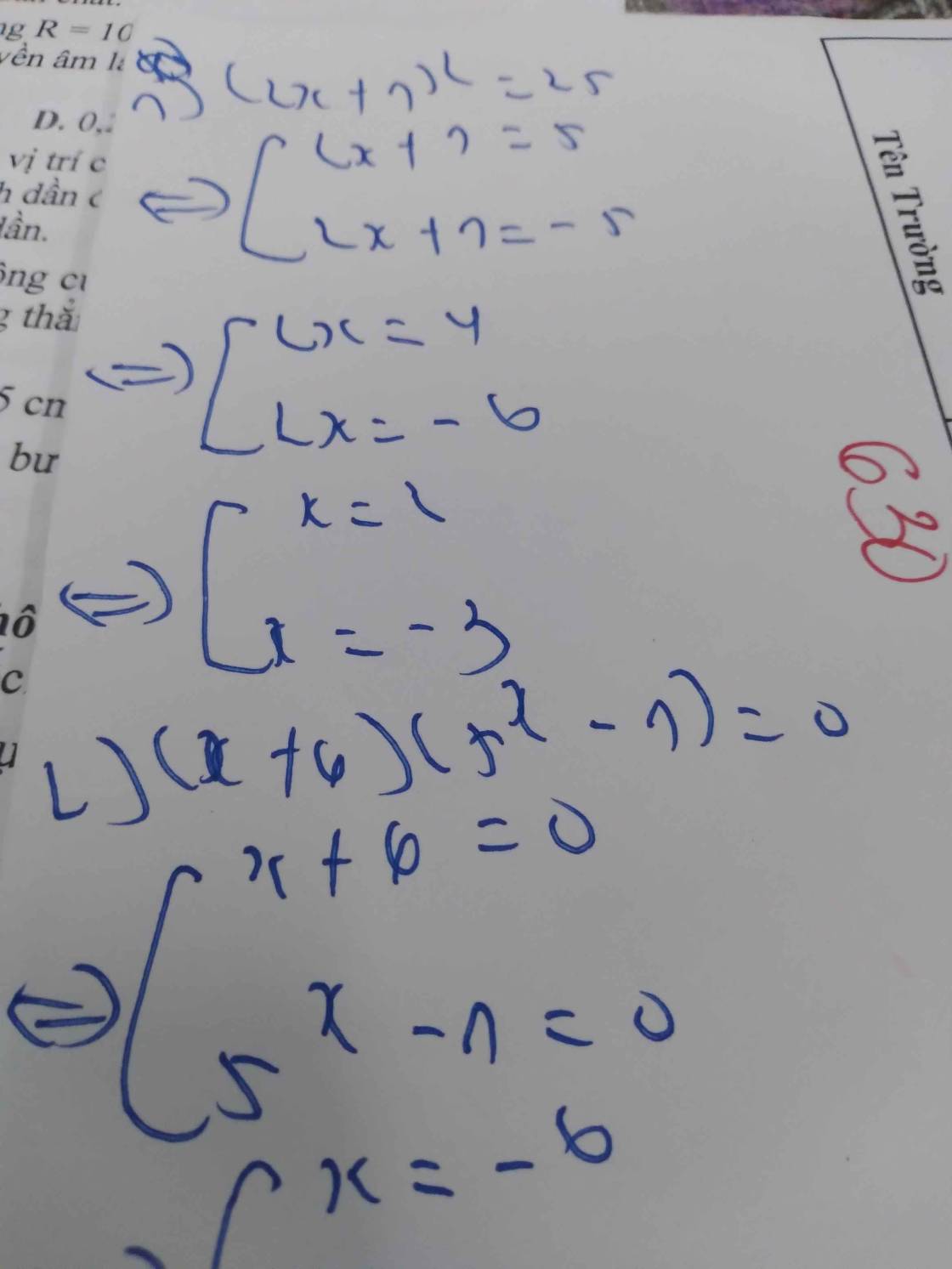
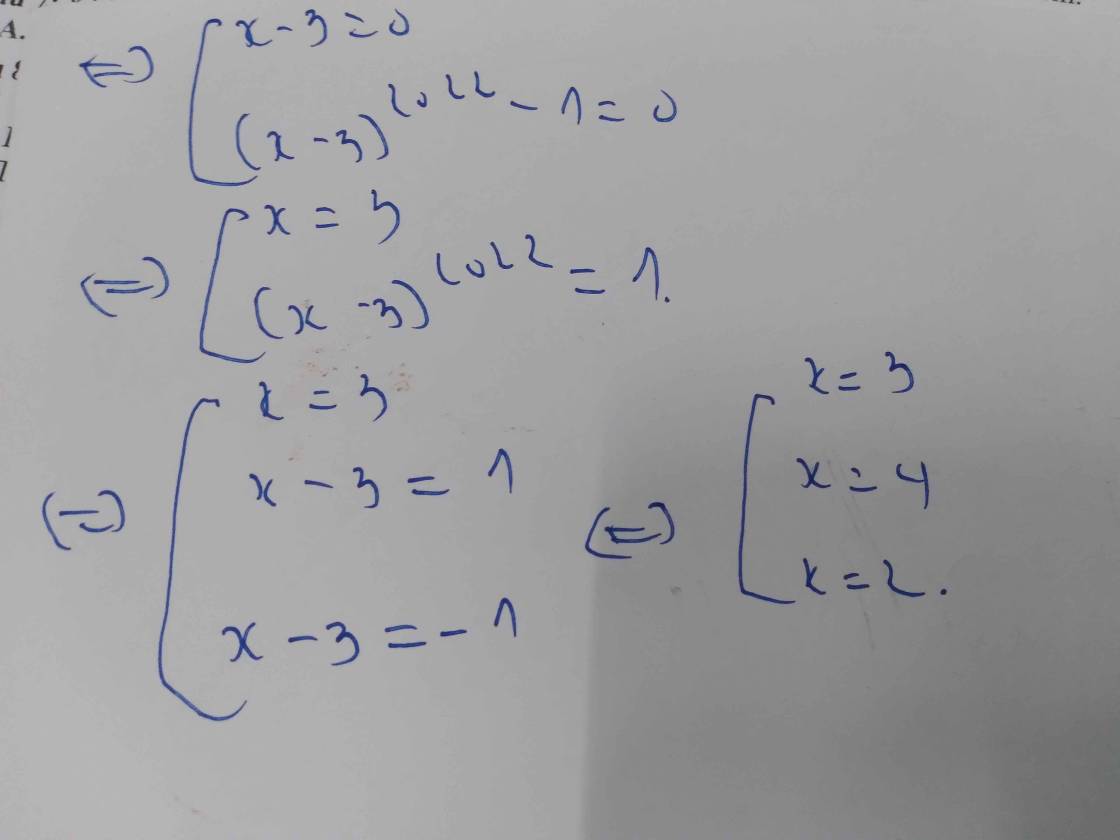
\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow x^3:\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^2\cdot\dfrac{1}{2}\)
\(\Rightarrow x^3=\left(\dfrac{1}{2}\right)^3\)
\(\Rightarrow x=\dfrac{1}{2}\)
\(x^3:\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\Rightarrow x^3=\dfrac{1}{2}.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}.\left(\dfrac{1}{2}\right)^2=\left(\dfrac{1}{2}\right)^3\)
\(\Rightarrow x=\dfrac{1}{2}\)