GTLN, GTNN của hàm số
y=x3 _ 3x2 - 9x + 35 trên đoạn [ -4,4] lần lược là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Xét hàm số y = x 3 + 3 x 2 - 9 x + 1 trên đoạn [-4;4].
Ta có:
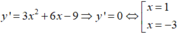
y(1) = -4, y(-3) = 28; y(4) = 77; y(-4) = 21
GTNN của hàm số y = x 3 - 9 x + 1 trên đoạn [-4;4] là -4 khi x= 1

Đáp án A.
Hàm số liên tục trên đoạn [-4;4]
y' = 3x2 – 6x – 9, y’ = 0 => x2 – 2x – 3 = 0 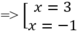
Ta có y(-4) = -41; y(4) = 15; y(-1) = 40; y(3) = 8
Vậy M = max[-4;4]y = 40 và m = min[-4;4]y = -41

Đáp án D
y ' = 3 x 2 - 6 x - 9
y ' = 0 ⇔ x = - 1 x = 3
y ( - 4 ) = - 41 , y ( 4 ) = 15 , y ( - 1 ) = 40 , y ( 3 ) = 8

Đáp án B
Ta có y ' = 3 x 2 − 6 x − 9 ⇒ y ' = 0 ⇔ x = − 1 x = 3
Suy ra y − 4 = − 41 , y − 1 = 40 , y 3 = 8 , y 4 = 15 ⇒ m ax − 4 ; 4 y = 40.

TXĐ: D = R.
y ' = 3 x 2 - 6 x - 9 ;
y' = 0 ⇔ x = –1 hoặc x = 3.
+ Xét hàm số trên đoạn [-4; 4] :
y(-4) = -41 ;
y(-1) = 40 ;
y(3) = 8
y(4) = 15.
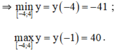
+ Xét hàm số trên [0 ; 5].
y(0) = 35 ;
y(3) = 8 ;
y(5) = 40.
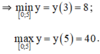
\(y=x^3-3x^2-9x+35\)
\(y'=3x^2-6x-9\)
\(y'=0\Leftrightarrow3x^2-6x-9=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(y\left(-4\right)=-41;y\left(-1\right)=40;y\left(3\right)=8;y\left(4\right)=52\)
\(\Rightarrow y_{max}=y\left(4\right)=52;y_{min}=y\left(-4\right)=-41\) trên đoạn \(\left[-4;4\right]\)