Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(sinx)4+(cosx)2+ 1 =>sinx4+sinx2 +2 => (sinx2-1/2)+3/4 => (((((Min = 3/4)))))
=> sinx=1/2

ta có
\(y'=3x^2-6x=3x\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
y' >0 khi \(x\in\left(-\infty,0\right)\cup\left(2,+\infty\right)\)
Vậy hàm đồng biến trên hai khoảng là \(\left(-\infty,0\right)\cup\left(2,+\infty\right)\)

1. Không rõ đề
2.
\(y'=\sqrt{x^2+3}+\frac{x\left(x-6\right)}{\sqrt{x^2+3}}=\frac{2x^2-6x+3}{\sqrt{x^2+3}}< 0;\forall x\in\left[1;2\right]\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left[1;2\right]\Rightarrow y_{max}=y\left(1\right)=-10\)
3.
\(y'=3x^2-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\frac{4m}{3}\end{matrix}\right.\)
Ta có: \(y\left(1\right)=3-3m\) ; \(y\left(3\right)=29-19m\)
TH1: \(\frac{4m}{3}\le1\Rightarrow m\le\frac{3}{4}\) khi đó hàm đồng biến trên \(\left[1;3\right]\Rightarrow y_{max}=y\left(3\right)\)
\(\Rightarrow29-19m=6\Leftrightarrow m=\frac{23}{19}>\frac{3}{4}\left(ktm\right)\)
TH2: \(\frac{4m}{3}\ge3\Rightarrow m\ge\frac{9}{4}\)
Khi đó hàm nghịch biến trên \(\left[1;3\right]\Rightarrow y_{max}=y\left(1\right)\)
\(\Rightarrow3-3m=6\Rightarrow m=-1< \frac{9}{4}\left(ktm\right)\)
TH3: \(1< \frac{4m}{3}< 3\Rightarrow\frac{3}{4}< m< \frac{9}{4}\)
Hàm nghịch biến trên \(\left(1;\frac{4m}{3}\right)\) và đồng biến trên \(\left(\frac{4m}{3};3\right)\)
\(\Rightarrow\) Hàm đạt GTLN tại \(x=1\) hoặc \(x=3\)
\(y\left(1\right)=3-3m=6\Rightarrow m=-1\notin\left(\frac{3}{4};\frac{9}{4}\right)\) (loại)
\(y\left(3\right)=29-19m=6\Rightarrow m=\frac{23}{19}\in\left(\frac{3}{4};\frac{9}{4}\right)\)
Vậy \(m=\frac{23}{19}\)

Giải:
(Hàm số không có tập xác định bao gồm \(0\) nên phải là \((0,3]\))
\(f'(x)=6x^2-\frac{6}{x^3}=\frac{6(x^5-1)}{x^3}=0\Leftrightarrow \) \(x=1\)
Bây giờ xét:
\(f(1)=10\)
\(f(3)=\frac{178}{3}\)
Vậy \(\left\{\begin{matrix} f_{\min}=10\Leftrightarrow x=1\\ f_{\max}=\frac{178}{3}\Leftrightarrow x=3\end{matrix}\right.\)

đáp án là :
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi
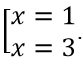
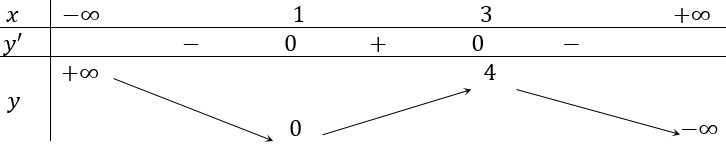
\(y=x^3-3x^2-9x+35\)
\(y'=3x^2-6x-9\)
\(y'=0\Leftrightarrow3x^2-6x-9=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(y\left(-4\right)=-41;y\left(-1\right)=40;y\left(3\right)=8;y\left(4\right)=52\)
\(\Rightarrow y_{max}=y\left(4\right)=52;y_{min}=y\left(-4\right)=-41\) trên đoạn \(\left[-4;4\right]\)