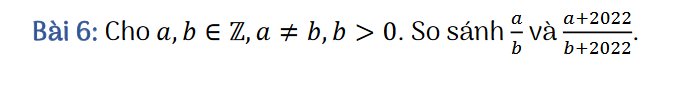
giúp em vớiiiiiiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 10 2021
a)+ Xét tứ giác ABFE có:
AB//FE (gt)
\(\Rightarrow\) Tứ giác ABFE là hình thang (định nghĩa hình thang)
+ Xét tứ giác CDHG có:
CD//HG (gt)
\(\Rightarrow\)Tứ giác CDHG là hình thang (định nghĩa hình thang)
b) Xét hình thang ABEF có:
C là trung điểm của AE
D là trung điểm của BF
\(\Rightarrow\)CD là đường trung bình của hình thang ABEF (định nghĩa đường trung bình của hình thang)
\(\Rightarrow\)CD=\(\dfrac{AB+EF}{2}\) (tính chất đường trung bình của hình thang)
hay CD=\(\dfrac{8+16}{2}\) = 12 (cm)
\(\Rightarrow\) x=12
+Xét hình thang CDHG có:
E là trung điểm của CG
F là trung điểm của DH
\(\Rightarrow\)EF là đường trung bình của hình thang CDHG (định nghĩa đường trung bình của hình thang)
\(\Rightarrow\)\(EF=\dfrac{CD+GH}{2}\) (tính chất đường trung bình của hình thang)
hay 16=\(\dfrac{12+GH}{2}\)
GH= 20 (cm)
\(\Rightarrow y=20\)
L
17 tháng 4 2022
a) Ta có x6 luôn luôn lớn hơn hoặc bằng 0 ; 9 < 0
=> x6 + 9 < 0 => đa thức đó không có nghiệm
b) Ta có 3x luôn luôn lớn hơn hoặc bằng 0 ; 15 < 0
=> 3x + 15 < 0 => đa thức đó không có nghiệm
c) Ta có x2 + x lớn hơn hoặc bằng 0 ; 2 < 0
=> x2 + x + 2 < 0 => đa thức đó không có nghiệm
P/s: khi trình bày thì cậu dùng các kí hiệu toán học thay vào chỗ "luôn luôn lớn hơn hoặc bằng" nhe :D
Q9
1
17 tháng 9 2017
Số số hạng là :
( 99 - 1 ) : 1 + 1 = 99 (SSH)
Tổng là :
( 99 + 1 ) x 99 : 2 = 4950
Đ/S : 4950
Chúc bạn học tốt ^_^
NT
1
TA
0
TA
1
HD
9 tháng 8 2021
Ta thấy rằng 2|y+1| luôn luôn lớn hơn 0
Nên suy ra được là : |x-3|+2(y+1)=6
<=>|x-3|+2y=4
<=>|x-3|=4-2y
Có hai trường hợp
1, x-3=4-2y
<=>x-7-2y=0
<=>x-2y=7
2, 3-x=4-2y
<=>x-2y=-1
Đến đây ta thấy hai kết quả khác hoàn toàn nên ko thảo mãn x và y
a,b \(\in\) Z, a \(\ne\) b, b > 0
So sánh: \(\dfrac{a}{b}\) và \(\dfrac{a+2022}{b+2022}\)
Có hai trường hợp:
+ Nếu a < b ta có:
\(\dfrac{a}{b}\) = 1 - \(\dfrac{b-a}{b}\) ; \(\dfrac{a+2022}{b+2022}\) = 1 - \(\dfrac{b-a}{b+2022}\)
Vì \(\dfrac{b-a}{b}\) > \(\dfrac{b-a}{b+2022}\)
Vậy : \(\dfrac{a}{b}\) < \(\dfrac{a+2022}{b+2022}\)
+ Nếu a > b ta có
\(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b}\); \(\dfrac{a}{b}\) = 1 + \(\dfrac{a-b}{b+2022}\)
Vì \(\dfrac{a-b}{b}\) > \(\dfrac{a-b}{b+2022}\)
Vậy \(\dfrac{a}{b}\) > \(\dfrac{a+2022}{b+2022}\)