Tính giá trị của biểu thức: A = x/21 + y/21 + z/21 biết x+y+z = 42
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
2
20 tháng 7 2016
Theo đầu bài ta có:
\(A=\frac{-5x}{21}+\frac{-5y}{21}+\frac{-5z}{21}\)
\(=\frac{-5x+-5y+-5z}{21}\)
\(=\frac{-5\left(x+y+z\right)}{21}\)
\(=\frac{-5\left(-z+z\right)}{21}\)
\(=\frac{-5\cdot0}{21}\)
\(=\frac{0}{21}=0\)
TM
20 tháng 7 2016
\(A=\frac{-5x}{21}+\frac{-5y}{21}+\frac{-5z}{21}\)
=>\(A=\frac{\left(-5x\right)+\left(-5y\right)+\left(-5z\right)}{21}\)
=>\(A=\frac{\left(-5\right)\left(x+y+z\right)}{21}\)
=>\(A=\frac{\left(-5\right)\left(-z+z\right)}{21}\)
=>\(A=\frac{\left(-5\right).0}{21}\)
=>\(A=\frac{0}{21}\)
=>A=0
MT
0
NM
0
PP
2
2 tháng 8 2019
A = \(\frac{-5x}{21}\)+ \(\frac{-5y}{21}\)+ \(\frac{-5x}{21}\)
= \(\frac{\left(-5x\right)+\left(-5y\right)+\left(-5x\right)}{21}\)
vì x + y là số dõi của z
=> x + y + z = 0
=> \(\frac{5.\left(x+y+z\right)}{21}\)
= \(\frac{-5}{21}\). 0 = 0
=> A = 0
hok tốt !
11 tháng 9 2021
Thay -z=x+y vào biểu thức A ta có A=-5x/21+(-5y/21)+[5(x+y)/21] =>-5x/21 +(-5y/21)+(5x+5y)/21=>-5x/21+(-5y/21)+5x/21+5y/21 => A = 0
DT
0
1 tháng 10 2017
\(\frac{\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)}{\frac{1}{x+y+x}}=1\Leftrightarrow\left(x+y+z\right)\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{x}\right)=1\)
\(\Leftrightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z}\)
\(\Rightarrow\left(\frac{1}{x}+\frac{1}{y}\right)+\left(\frac{1}{z}-\frac{1}{x+y+z}\right)=0\)
\(\Leftrightarrow\frac{x+y}{xy}+\frac{x+y}{z\left(x+y+z\right)}=0\)\(\Leftrightarrow\left(x+y\right)\left[z\left(x+y+z\right)+xy\right]=0\)
\(\Leftrightarrow\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)
B=\(\left(x+y\right)\left(y+z\right)\left(z+x\right).M=0\)
26 tháng 8 2020
a, A=xy+7x-3y-21 b,B= xyz+xz-yz-z+xy+x-y-1
A=(xy+7x)-(3y+21) B=(xyz+xz)-(yz+z)+(xy+x)-(y+1)
A=x(y+7)-3(y+7) B=xz(y+1)-z(y+1)+x(y+1)-(y+1)
A=(y+7)(x-3) B=(y+1)(xz-z+x-1)
Thay x=103, y=-17 vào biểu thức ta có: B=(y+1)[(xz-z)+(x-1)]
A=(-17+7)(103-3) B=(y+1)[z(x-1)+(x-1)]
A=(-10)(100) B=(y+1)(x-1)(z+1)
A=-1000 Thay x=-9, y=-21, z=-31 vào biểu thức ta có:
B=(-21+1)(-9-1)(-31+1)
B=(-20)(-10)(-30)
B=200(-30)
B=-6000
YN
30 tháng 3 2022
`Answer:`
\(A=\frac{-5x}{21}+\frac{-5y}{21}+\frac{-5z}{21}\)
\(=\frac{-5x-5y-5z}{21}\)
\(=\frac{-5\left(x+y\right)-5z}{21}\)
\(=\frac{-5\left(-z\right)-5z}{21}\)
\(=\frac{5z-5z}{21}\)
\(=\frac{0}{21}\)
\(=0\)
CM
27 tháng 2 2019
Đáp án C.
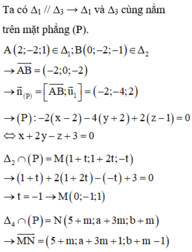
Không tồn tại đường thẳng nào trong không gian cắt cả 4 đường thẳng đã cho
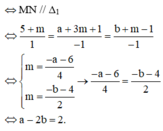
`A = x/21 + y/21 + z/21.`
`= (x+y+z)/21 = 42/21 = 2`.
Vậy `A =2.`