Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
N
11 tháng 11 2021
\(1min=60s\)
\(\Rightarrow f=\dfrac{720}{60}=12\left(vong/s\right)=12\left(Hz\right)\)
31 tháng 10 2021
Một quạt máy quay với tần số 450/ vòng/phút cánh quạt dài 0,8 m. Tính;tốc độ góc tốc độ dài của một điểm ở đầu cánh quạt
18 tháng 11 2021
\(f=240\)vòng/phút=4vòng/s
\(\Rightarrow\)Chu kì: \(T=\dfrac{1}{f}=\dfrac{1}{4}s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{1}{4}}=8\pi\)(rad/s)
Tốc độ dài: \(v=\omega\cdot R=8\pi\cdot0,4=10,05\)m/s
Gia tốc hướng tâm:
\(a_{ht}=r\cdot\omega^2=0,4\cdot\left(8\pi\right)^2\approx252,66\)m/s2
12 tháng 11 2021
\(f=450\)vòng/phút=7,5 vòng/s
\(R=80cm=0,8m\)
+Chu kì quay của cánh quạt:
\(T=\dfrac{1}{f}=\dfrac{1}{7,5}=\dfrac{2}{15}s\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{\dfrac{2}{15}}=15\pi\)(rad/s)
+Tốc độ dài:
\(v=\omega\cdot R=15\pi\cdot0,8=12\pi\)(m/s)
+Gia tốc hướng tâm:
\(a_{ht}=R\cdot\omega^2=0,8\cdot\left(15\pi\right)^2\approx1776,53\)m/s2
VT
18 tháng 11 2019
Ta có:
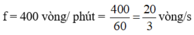
Tốc độ góc của một điểm bất kì ở đầu cánh quạt là:
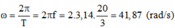
Tốc độ dài của điểm trên đầu cánh quạt là: V = R.ω = 33,5 m/s.
16 tháng 4 2017
Ta có: Tần số quạt máy quay
+ f = 400 vòng / phút = vòng/ s =
vòng/s
+ R = 0,8 m
+ Vận tốc dài v = ωR và ω = 2πf => v = 2πfR
=> v = 2. 3,14. = 41,866 rad/s
=> ω ≈ 41,87 rad/s
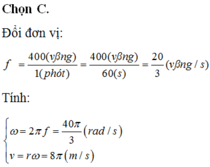
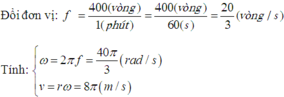
Trong 3s, quạt quay được: \(3\cdot\dfrac{45}{60}=\dfrac{9}{4}\left(vòng\right)\)
Vậy quạt quay được 1 góc: \(2\pi\cdot\dfrac{9}{4}=\dfrac{9\pi}{2}\left(rad\right)\)
Trong 3 giây quay được:
3*45/60=9/4(vòng)
Số đo góc quay được:
2pi*9/4=9/2*pi