Hình vuông ABCD, M là trung điểm của AB, N là điểm trên cạnh AC sao cho AN=3NC. Chứng minh AMN là tam giác vuông cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

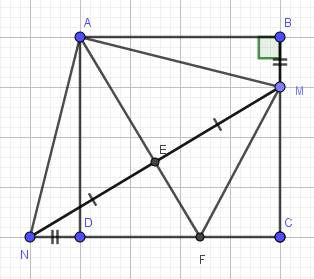
a) Do ABCD là hình vuông (gt)
\(\Rightarrow AB=AD\)
\(\widehat{ABM}=\widehat{ADN}=90^0\)
Xét hai tam giác vuông: \(\Delta ABM\) và \(\Delta ADN\) có:
\(AB=AD\left(cmt\right)\)
\(BM=DN\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta ADN\) (hai cạnh góc vuông)
\(\Rightarrow AM=AN\) (hai cạnh tương ứng)
\(\widehat{BAM}=\widehat{DAN}\) (hai góc tương ứng)
Ta có:
\(\widehat{BAM}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{DAN}+\widehat{DAM}=90^0\)
\(\Rightarrow\widehat{MAN}=90^0\)
\(\Delta AMN\) có:
\(AM=AN\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) cân tại A
Mà \(\widehat{MAN}=90^0\left(cmt\right)\)
\(\Rightarrow\Delta AMN\) vuông cân tại A
b) Do \(\Delta AMN\) cân tại A
E là trung điểm của MN
\(\Rightarrow AE\) là đường trung tuyến, cũng là đường cao của \(\Delta AMN\)
\(\Rightarrow AE\perp MN\)
\(\Rightarrow EF\perp MN\)
Xét hai tam giác vuông: \(\Delta FEM\) và \(\Delta FEN\) có:
\(EM=EN\left(gt\right)\)
\(EF\) là cạnh chung
\(\Rightarrow\Delta FEM=\Delta FEN\) (hai cạnh góc vuông)
\(\Rightarrow FM=FN\) (hai cạnh tương ứng)
Xét \(\Delta FAN\) và \(\Delta FAM\) có:
\(FA\) là cạnh chung
\(FN=FM\left(cmt\right)\)
\(AN=AM\left(cmt\right)\)
\(\Rightarrow\Delta FAN=\Delta FAM\left(c-c-c\right)\)

#)Góp ý :
Bạn tham khảo nhé :
gọi giao điểm của AC và BD là O
gọi H là trung điểm của OD
Do AN =3NC và O là trung điểm AC
=> N là trung điểm của OC
=> NH là đường trung bình của tam giác OCD
=> NH // CD // AB và NH = 1/2 CD = 1/2 AB = AM
=> AMNH là hình bình hành
=> MN // AH (1)
Lại có: trong tam giác ADN có AO vuong AN và NH vuông AD
=> H là trực tâm tam giác ADN
=> AH vuong ND (2)
Từ (1)(2) => MN vuông ND
=> tam giac DNM vuong tại N
Kéo dài NH cắt AD tại K
Rõ ràng tam giác AKN là tam giác vuông cân (do gocKAN = 45)
=> AK = KN
=> 2 tam giac vuông AHK và NDK bằng nhau (gcg)
=> AH = ND
mà AH = MN (do AMNH là hình bình hành)
=> MN = ND
=> tam giac DMN vuông cân tại N
Nguồn : Cho hình vuông ABCD có M là trung điểm của AB, N thuộc đoạn AC sao cho NA = 3NC. Chứng minh tam giác DMN vuông cân tại N. Tính độ dài cạnh của hình vuông biết MN = √10 - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục
Link : https://lazi.vn/edu/exercise/cho-hinh-vuong-abcd-co-m-la-trung-diem-cua-ab-n-thuoc-doan-ac-sao-cho-na-3nc-chung-minh-tam-giac-dmn

nè câu a) CM : BD=CE
mà sao đề cho BO
mình làm theo BD nhé
a) xét tam giác zuông BEC zà tam giác zuông BDC có
\(\hept{\begin{cases}ch:BC\left(chung\right)\\gn:\widehat{EBC}=\widehat{DCB}\left(ABCcân\right)\end{cases}}\)
=> 2 tam giác zuông trên = nhau nha
=>EB=DC
+) xét tam giác zuông BEH zà tam giác zuông DHC có
\(\hept{\begin{cases}gn:\widehat{EHB}=\widehat{DHC}\left(đđ\right)\\cgz:EB=DC\left(cmt\right)\end{cases}}\)
=> 2 tam giác zuông kia = nhau
=> BD=CE
b) câu b ghi đề trả hiểu j

a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAMD và ΔANB có
AM=AN
MD=NB
AD=AB
Do đó: ΔAMD=ΔANB

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
Đề bài phải sửa thành AN=NC mới c/m được
MA=MB (gt)
AN=NC (gt)
=> MN là đường trung bình của tg ABC
=> MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có
\(BC\perp AB\) mà MN//BC => \(MN\perp AB\) (1)
Ta có
\(BC=AB\Rightarrow MN=\dfrac{AB}{2}\)
Mà \(MA=MB=\dfrac{AB}{2}\)
=> MN = MA (2)
Từ (1) và (2) => tg AMN vuông cân tại M