Xét dãy ( Un ) ; n = 1,2,3,.... xác định bởi U0 = 2, Un = 3Un-1 + 2n3 - 9n2 + 9n - 3
a) Lập quy trình tính Un ?
b) Tính U20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dãy số ( u n ) với u n = n 2 n
Dễ thấy u n > 0 ∀ n ∈ N ∗ . Xét tỉ số: u n u n + 1
Ta có: u n u n + 1 = n 2 n . 2 n + 1 n + 1 = 2 n n + 1 > 1 ∀ n ≥ 1
Thật vậy: 2 n n + 1 > 1 ⇔ 4 n n + 1 > 1 ⇔ 4 n > n + 1 ⇔ 3 n > 1 ( đúng ∀ n ≥ 1 )
Do đó, u n > u n + 1 nên ( u n ) là một dãy số giảm.
Chọn đáp án B.

Xét hiệu:
u n + 1 − u n = 1 n + 1 − 2 − 1 n − 2 = 1 n + 1 − 1 n = − 1 n ( n + 1 ) < 0 ∀ n ∈ ℕ *
Kết luận dãy số ( u n ) là dãy số giảm.
Chọn đáp án B


Ta có u n = n − 1 n + 1 = 1 − 2 n + 1
Xét hiệu u n + 1 − u n = 1 − 2 n + 2 − 1 − 2 n + 1
= 2 n + 1 − 2 n + 2 = 2 ( n + 2 ) − 2 ( n + 1 ) ( n + 1 ) . ( n + 2 ) = 2 ( n + 1 ) ( n + 2 ) > 0 ∀ n ∈ ℕ *
Kết luận dãy số ( u n ) là dãy số tăng.
Chọn đáp án D.

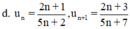
với n ∈ N*, n ≥ 1
Xét:
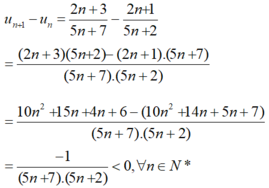
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm

Rõ ràng u n > 0 , ∀ n ∈ ℕ * nên ( u n ) bị chặn dưới.
Lại có: 1 k k + 1 = 1 k − 1 k + 1 .
Suy ra u n = 1 − 1 2 + 1 2 − 1 3 + ... + 1 n − 1 n + 1 = 1 − 1 n + 1 < 1 , ∀ n ∈ ℕ * nên ( u n ) bị chặn trên.
Kết luận ( u n ) bị chặn.
Chọn đáp án C.

un = (-1)n.(2n + 1)
Nhận xét: u1 < 0, u2 > 0, u3 < 0, u4 > 0, …
⇒ u1 < u2, u2 > u3, u3 < u4, …
⇒ dãy số (un) không tăng, không giảm.