[ Tổng hợp kiến thức Toán Học dành cho HỌC SINH THCS (Part 3) ]
|-----------------------------------------------------------------------------|

#Lưu ý: Khi đọc các mục dưới đây chỉ có thể giúp các bạn cải thiện kiến thức môn Toán của mình và không bị "Mất gốc" trong môn Toán ở cấp độ THCS
(1) Phần số học:
+ Các tính chất cơ bản giao hoán, kết hợp
- Tính chất giao hoán được biểu hiện trong phép cộng và nhân
CT: \(a+b+c=a+c+b\)
\(a\cdot b\cdot c=a\cdot c\cdot b\)
Tính chất này khá quen ở cấp tiểu học và rất quan trọng ở cấp THCS
- Tính chất kết hợp được biểu hiện ở trong phép cộng và nhân
CT: \(a+b+c=\left(a+c\right)+b\)
\(a\cdot b\cdot c=\left(a\cdot c\right)\cdot b\)
Tương tự giao hoán tính chất này rất quan trong để làm các dạng bài tập như:
VD: \(3,12+6+0,88=\left(3,12+0,88\right)+6=4+6=10\)
+ Dấu hiệu chia hết cho các số từ 1 - 10
- Tất cả các số chia hết cho 1
- Chia hết cho 2:
Các số chia hết cho 2 có các chữ số cuối cùng là 0, 2, 4, 6, 8
VD: 12, 56, 96, ...
- Chia hết cho 3:
Dấu hiệu của một số chia hết cho 3 là tổng các chữ số đó sẽ chia hết cho 3:
CT: \(\overline{abcd}\) chia hết cho 3 khi \(a+b+c+d\) chia hết cho 3
VD: \(3210\) chia hết cho 3 vì \(3+2+1+0=6\) ⋮ 3
- Chia hết cho 4:
Dấu hiệu của 1 số chia hết cho 4 khi 2 chữ số cuối cùng của số đó chia hết cho 4 đều này bắt buộc các bạn phải nhớ được các số chia hết cho 4 từ 0 - 99
CT: \(\overline{abcd}\) chia hết cho 4 khi \(\overline{cd}\) chia hết cho 4
VD: \(3456\) chia hết cho 4 khi 56 chia hết cho 4
- Chia hết cho 5:
Dấu hiệu chia hết cho 5 là các số có chữ số cuối cùng là 5 hoặc 0
- Chia hết cho 6:
Dấu hiệu của một số chia hết cho 6 là số đó vừa chia hết cho 2 vừa chia hết cho 3
VD: 1230 chia hết cho 6 vì 1230 vừa chia hết cho 2 vừa chia hết cho 3
- Chia hết cho 7:
Dấu hiệu của 1 số chia hết cho 7 là lấy 5 nhân cho chữ số tận cùng rồi cộng cho phần còn lại của số đó nếu chia hết cho 7 thì số đó chia hết cho 7
CT: \(\overline{abcd}\)chia hết cho 7 khi \(5\cdot d+\overline{abc}\) ⋮ 7
VD: 182 chia hết cho 7 vì \(5\cdot2+18=28\) ⋮ 7
- Chia hết cho 8
Dấu hiệu 1 số chia hết cho 8 khi 3 chữ số cuối của số đó chia hết cho 8
VD: 1264 chia hết cho 8 khi 3 chữ số cuối của nó chia hết cho 8
- Chia hết cho 9
Dấu hiệu của 1 số chia hết cho 9 khi tổng các chữ số của số đó tạo thành 1 số chia hết cho 4
CT: \(\overline{abcd}\) chia hết cho 8 khi \(a+b+c+d\) ⋮ 9
VD: 36 chia hết cho 9 vì 3 + 6 chia hết cho 9
- Chia hết cho 10
Dấu hiệu chia hết cho 10 là chữ số tận cùng của số đó là số 0
VD: 120 chia hết cho 10 vì có chữ số tận cùng là số 0
+ Quy tắc dấu của các phép cộng trừ nhân chia các số nguyên
- Phép cộng:
\(a+b=a+b\)
\(\left(-a\right)+\left(-b\right)=-\left(a+b\right)\)
\(a+\left(-b\right)=a-b\)
\(-a+b=b-a\)
- Phép trừ:
\(a-b=a-b\)
\(-a-b=-\left(a+b\right)\)
\(a-\left(-b\right)=a+b\)
- Phép nhân:
\(a\cdot b=a\cdot b\)
\(-a\cdot-b=a\cdot b\)
\(a\cdot-b=-\left(a\cdot b\right)\)
\(-a\cdot b=-\left(a\cdot b\right)\)
- Phép chia:
\(a:b=a:b\)
\(-a:-b=a:b\)
\(-a:b=-\left(a:b\right)\)
\(a:-b=-\left(a:b\right)\)
Lưu ý: Khi mở/ đóng ngoặc nếu trước dấu ngoặc đó là dấu + thì dữ nguyên nếu trước dấu ngoặc đó là dấu - thì đổi dấu tất cả hạng tử của phép tính đó:
VD: \(-\left(a-b-c\right)=-a+b+c\)
+ Tính chất dãy tỉ số bằng nhau
Ta có tính chất này:
Nếu: \(\dfrac{a}{m}=\dfrac{b}{n}\) (với m,n là số nguyên ≠ biến) và biết \(a\pm b=?\) thì ta có thể tìm được a,b như sau:
VD: \(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{a+b}{2+3}=\dfrac{5}{5}=1\) (biết \(a+b=5\))
\(\Rightarrow\left\{{}\begin{matrix}a=2\cdot1=2\\b=3\cdot1=3\end{matrix}\right.\)
Công thức tổng quát: \(\dfrac{a_1}{m_1}=\dfrac{a_2}{m_2}=\dfrac{a_3}{m_3}=...=\dfrac{a_n}{m_n}=\dfrac{a_1+a_2+...+a_n}{m_1+m_2+...+m_n}\)
(2) Phần hình học
+ Các trường hợp bằng nhau của tam giác
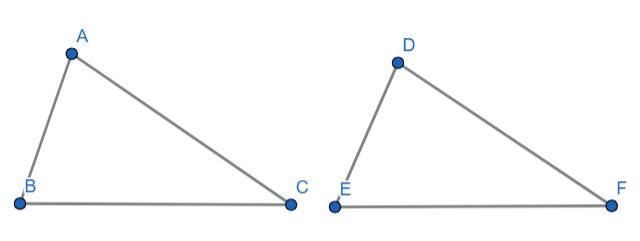
- Trường hợp 1:
Nếu 3 cạnh của tam giác này bằng 3 cạnh của tam giác kia thì 2 tam giác này bằng nhau
Xét ΔABC và ΔDEF ta có:
\(AB=DE\left(gt\right)\)
\(AC=DF\left(gt\right)\)
\(BC=EF\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.c.c\right)\)
- Trường hợp 2:
Nếu 2 cạnh của tam giác này bằng 2 cạnh của tam giác kia và 1 góc nằm giữa 2 cạnh này của tam giác này bằng góc nằm giữa 2 cạnh này của tam giác kia thì hai tam giác bằng nhau
Xét ΔABC và ΔDEF ta có:
\(AB=DE\left(gt\right)\)
\(AC=DF\left(gt\right)\)
\(\widehat{A}=\widehat{D}\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(c.g.c\right)\)
- Trường hợp 3:
Nếu 1 cạnh của tam giác này bằng 1 cạnh của tam giác kia và 2 góc kề cạnh này của tam giác này bằng 2 góc kề cạnh này của tam giác kia thì hai tam giác bằng nhau
Xét ΔABC và ΔDEF ta có:
\(\widehat{A}=\widehat{D}\left(gt\right)\)
\(AB=DE\left(gt\right)\)
\(\widehat{B}=\widehat{E}\left(gt\right)\)
\(\Rightarrow\text{Δ}ABC=\text{Δ}DEF\left(g.c.g\right)\)
+ Định lý Py-ta-go thuận và đảo
- Theo định lý Py-ta-go thì trong 1 tam giác vuông thì tổng bình phương của hai cạnh góc vuông bằng bình phương của cạnh huyền (nhận biết cạnh huyền: cạnh đối diện với góc vuông thì cạnh đó là cạnh huyền
Theo ĐL Py-ta-go trong tam giác vuông: \(a^2+b^2=c^2\) (1) (a,b là cạnh góc vuông, c là cạnh huyền)
Từ công thức thên ta có thể tính được toàn bộ các cạnh của tam giác vuông khi biết 2 cạnh còn lại
Từ (1) \(\Rightarrow\left\{{}\begin{matrix}c=\sqrt{a^2+b^2}\\a=\sqrt{c^2-b^2}\\b=\sqrt{c^2-a^2}\end{matrix}\right.\)
- Định lý Py-ta-go đảo được dựa trên định lý Py-ta-go thuận nên nếu trong 1 tam giác bình phương của cạnh này bằng tổng bình phương của 2 cạnh còn lại thì tam giác đó là tam giác vuông (góc đối diện với cạnh bằng tổng bình phương hai cạnh kia chính là góc vuông)
Theo định lý Py-ta-go đảo: \(c^2=a^2+b^2\Rightarrow\text{Δ}\) đó vuông
VD: Cho tam giác ABC vuông tại A và AB=3(cm), AC=4(cm). Tính BC
Xét ΔABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC^2=AC^2+AB^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{3^2+4^2}=\sqrt{25}=5\left(cm\right)\)
+ Bộ 3 độ dài cạnh của tam giác
Để xác định được bộ 3 độ dài cạnh của tam giác thì ta có nhận xét sau:
\(\left\{{}\begin{matrix}a+b>c\\a+c>b\\b+c>a\end{matrix}\right.\Rightarrow a,b,c\) là bộ 3 độ dài cạnh của tam giác
VD: cho tam giác ABC có: AB = 1(cm), AC=1,5(cm), BC=5(cm)
Ta có:
\(\left\{{}\begin{matrix}AB+AC< BC\left(1+1,5< 5\right)\\BC+AB>AC\left(1+5>15\right)\\BC+AC>AB\left(5+1,5>1\right)\end{matrix}\right.\)
Vậy bộ 3 độ dài của của tam giác ABC là không đúng
________________________________________
*Cách học môn toán không bị nhàm chán và thú vi cần biết các tips sau: *
- Không được học liên tiếp 2 - 3 giờ sẽ khiến cho cơ thể mệt mỏi buồn ngủ không hiệu quả
- Để không bị mất gốc thì nên học toàn chú trọng vào các ý chính (VD: ghi nhớ, các điều mà thầy cô lưu ý học)
- Không cần thuộc lòng quan trọng là biết vận dụng vào bài toán
- Cần lưu ý các kiến thức toán cở cấp độ của mình (tiểu học, THCS, THPT)
- Phối hợp việc học toán và việc giải trí tránh bị nhàm chán mất tinh thần
- Sử dụng sơ đồ tư duy, takennotes, ...
- Lại đi làm lại nhiều lần dạng bài còn yếu
- Ôn lại nhiều lần các kiến thức, khái niệm, công thức...
- Sử dụng nhiều kĩ thuật nhớ lâu, nhanh
Các bạn hay anh chị có các tips học toán thú vị hơn mong anh chị bình luận ở đây nhé (trân trọng)
(* Nếu trong part 3 này có gì thiếu sót thì mong các anh chị và các bạn góp ý với mình nhé mình sẽ cải thiện điều đó trong các part tới ạ *)





\(3.sin3x-4.cos3x=5\)
Ta có: 32 + (-4)2 = 52 . Chia pt cho \(\sqrt{3^2+\left(-4\right)^2}=5\) ta được:
\(\frac{3}{5}.sin3x-\frac{4}{5}.cos3x=1\) (1)
Đặt \(cos\alpha=\frac{3}{5},sin\alpha=\frac{4}{5}\) (1) trở thành:
\(sin\left(3x-\alpha\right)=sin\pi\)
\(\Rightarrow\orbr{\begin{cases}3x-\alpha=\pi+k2\pi\Rightarrow x=\frac{\pi+\alpha}{3}+\frac{k2\pi}{3}\\3x-\alpha=\pi-\pi+k2\pi\Rightarrow x=\frac{\alpha}{3}+\frac{k2\pi}{3}\end{cases}}\)
Vậy \(x=\left\{\frac{\pi+\alpha}{3}+\frac{k2\pi}{3};\frac{\alpha}{3}+\frac{k2\pi}{3}\right\}\)
tui học rùi...