K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 10 2020
ĐKXĐ:
a.
\(sin3x-sinx\ne0\)
\(\Leftrightarrow sin3x\ne sinx\Leftrightarrow\left\{{}\begin{matrix}3x\ne x+k2\pi\\3x\ne\pi-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
b.
\(cos3x-cosx\ne0\Leftrightarrow cos3x\ne cosx\)
\(\Leftrightarrow\left[{}\begin{matrix}3x\ne x+k2\pi\\3x\ne-x+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ne k\pi\\x\ne\frac{k\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\)
HN
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 9 2020
\(A=\frac{cos3x+cos9x+cos5x+cos7x}{sin3x+sin9x+sin5x+sin7x}=\frac{2cos6x.cos3x+2cos6x.cosx}{2sin6x.cos3x+2sin6x.cosx}\)
\(=\frac{2cos6x\left(cos3x+cosx\right)}{2sin6x\left(cos3x+cosx\right)}=tan6x\)
\(A=1\Rightarrow tan6x=1\Rightarrow x=\frac{\pi}{24}+\frac{k\pi}{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2021
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)
HP
28 tháng 8 2021
a, Vì \(-5sinx\ge-5\Rightarrow m-5sinx\ge0\forall x\Leftrightarrow m\ge5\)
b, Vì \(cos2x\ge-1\Rightarrow2m+cos2x\ge0\forall x\Leftrightarrow2m\ge1\Leftrightarrow m\ge\dfrac{1}{2}\)
c, TH1: \(m=0\) thỏa mãn yêu cầu bài toán
TH2: \(m>0\)
Khi đó: \(-m+1\le mcosx+1\le m+1\)
Yêu cầu bài toán thỏa mãn khi \(-m+1>0\Leftrightarrow m< 1\)
\(\Rightarrow0< m< 1\)
TH3: \(m< 0\)
Khi đó: \(m+1\le mcosx+1\le-m+1\)
Yêu cầu bài toán thỏa mãn khi \(m+1>0\Leftrightarrow m>-1\)
\(\Rightarrow-1< m< 0\)
Vậy \(m\in\left(-1;1\right)\)
TN
1
29 tháng 9 2020
Đề thiếu bạn nhé!
\(5(sinx+\frac{cos3x+sin3x}{1+2sin2x})=cos2x+3\) (*)
ĐKXĐ: 1 + 2sin2x \(\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x\ne-\frac{\pi}{12}+k\pi\\x\ne\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
Biến đổi riêng biểu thức: \(\frac{cos3x+sin3x}{1+2sin2x}\)
= \(\frac{\left(4cos^3x-3cosx\right)+\left(3sinx-4sin^3x\right)}{1+2sin2x}\)
\(=\frac{4\left(cos^3x-sin^3x\right)+3\left(sinx-cosx\right)}{1+2sin2x}\)
\(=\frac{4\left(cosx-sinx\right)\left(cos^2x+sinx.cosx+sin^2x\right)-3\left(cosx-sinx\right)}{1+2sin2x}\)
= \(\frac{4\left(cosx-sinx\right)\left(1+sinx.cosx\right)-3\left(cosx-sinx\right)}{1+2sin2x}\)
= \(\frac{\left(cosx-sinx\right)\left(4+2sin2x-3\right)}{1+2sin2x}\)
= cosx - sinx
Khi đó:
(*) \(\Leftrightarrow\) 5(sinx + cosx - sinx) - cos2x - 3 = 0
\(\Leftrightarrow5cosx+1-2cos^2x-3=0\)
\(\Leftrightarrow2cos^2x-5cosx+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=2\left(-1\le cosx\le1\right)\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\frac{\pi}{3}+k2\pi\)
Với x \(\in\left[0;2\pi\right]\Leftrightarrow\left[{}\begin{matrix}0\le\frac{\pi}{3}+k2\pi\le2\pi\\0\le-\frac{\pi}{3}+k2\pi\le2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-\frac{1}{6}\le k\le\frac{5}{6}\\\frac{1}{6}\le k\le\frac{7}{6}\end{matrix}\right.\)
k \(\in Z\Rightarrow\left[{}\begin{matrix}k=0\\k=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}\\x=\frac{5\pi}{3}\end{matrix}\right.\)
Nghiệm của pt (*) thuộc đoạn [0;\(2\pi\)] là:
S = \(\left\{\frac{\pi}{3};\frac{5\pi}{3}\right\}\)
21 tháng 7 2022
b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)
c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)
\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)
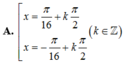
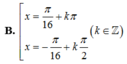
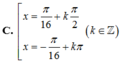
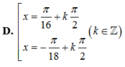
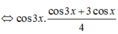
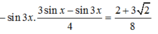
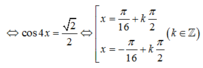
Yêu cầu bài toán?