Tìm các cặp số nguyên (x,y)biết : 2xy+x -4y=8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, (3 - \(x\))(4y + 1) = 20
Ư(20) = { -20; -10; -5; -4; -2; -1; 1; 2; 4; 5; 10; 20}
Lập bảng ta có:
| \(3-x\) | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| \(x\) | 23 | 13 | 8 | 7 | 5 | 4 | 2 | 1 | -1 | -2 | -7 | -17 |
| 4\(y\) + 1 | -1 | -2 | -4 | -5 | -10 | -20 | 20 | 10 | 5 | 4 | 2 | 1 |
| \(y\) | -1/2 | -3/4 | -5/4 | -6/4 | -11/4 | -21/4 | 19/4 | 9/4 | 1 | 3/4 | 1/4 | 0 |
Vậy các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) =(-1; 1); (-17; 0)
b, \(x\left(y+2\right)\)+ 2\(y\) = 6
\(x\) = \(\dfrac{6-2y}{y+2}\)
\(x\in\) Z ⇔ 6 - \(2y⋮\) \(y\) + 2 ⇒-(2y + 4) +10 ⋮ \(y\) + 2 ⇒ -2(\(y\)+2) +10 ⋮ \(y\)+2
⇒ 10 ⋮ \(y\) + 2
Ư(10) = { -10; -5; -2; -1; 1; 2; 5; 10}
Lập bảng ta có:
| \(y+2\) | -10 | -5 | -2 | -1 | 1 | 2 | 5 | 10 |
| \(y\) | -12 | -7 | -4 | -3 | -1 | 0 | 3 | 8 |
| \(x=\) \(\dfrac{6-2y}{y+2}\) | -3 | -4 | -7 | -12 | 8 | 3 | 0 | -1 |
Theo bảng trên ta có các cặp \(x;y\)
nguyên thỏa mãn đề bài lần lượt là:
(\(x;y\) ) =(-3; -12); (-4; -7); (-12; -3); (8; -1); (3; 0); (0;3 (-1; 8)


Ta có : 2xy + x - 4y = 7
=> 2(2xy + x - 4y) = 7.2
=> 4xy + 2x - 8y = 14
=> (4xy - 8y) + 2x - 4 = 14 - 4
=> 4y(x - 2) + 2(x - 2) = 10
=> ( 4y + 2)(x - 2) = 10
=> 4y + 2;x - 2 ∈ Ư(10) ∈ {-10;-5;-2;-1;1;2;5;10}
Mà 4y + 2 luôn chẵn => Ta có bảng sau :
| 4y + 2 | -10 | 10 | 2 | -2 |
| x - 2 | -1 | 1 | 5 | -5 |
| y | -3 | 2 | 0 | -1 |
| x | 1 | 3 | 7 | -3 |

6xy+4x-3y=8
=> 6xy -3y=8-4x
=>3y(2x-1)= -2(2x-1) +6
=>(2x-1)(3y+2)=6
mà x,y thuộc Z =>(2x-1),(3y+2) thuộc Z =>(2x-1),(3y+2) thuộc U(6) xong giải ra bình thường nhé mấy câu sau tương tự

Do \(x,y,z\inℤ\)
nen tu gia thiet suy ra
\(x^2+4y^2+z^2-2xy-2y+2z\le-1\)
\(\Leftrightarrow\left(x-y\right)^2+\left(z+1\right)^2+\left(y-1\right)^2+2y^2\le1\)
mat khac
\(\hept{\begin{cases}\left(y-1\right)^2+2y^2>0\\\left(x-y\right)^2+\left(z+1\right)^2\ge0\end{cases}}\)
nen \(\left(x-y\right)^2+\left(z+1\right)^2+\left(y-1\right)^2+2y^2=1\)
den day ban lap bang cac gia tri se tim duoc \(\left(x,y,z\right)=\left(0,0,-1\right)\)

\(x-2xy+y=0\Rightarrow2\left(x-2xy+y\right)=0\Rightarrow2x-4xy+2y=0\)
\(\Rightarrow2x\left(1-2y\right)+2y-1=2x\left(1-2y\right)-\left(1-2y\right)=-1\Rightarrow\left(2x-1\right)\left(1-2y\right)=-1\)
\(\Rightarrow2x-1;1-2y\inƯ\left(1\right)\Rightarrow2x-1;1-2y=+-1\)
\(2x-1=1\Rightarrow2x=2\Rightarrow x=1\)thì \(1-2y=-1\Rightarrow-2y=-2\Rightarrow y=1\)
\(2x-1=-1\Rightarrow2x=0\Rightarrow x=0\)thì \(1-2y=1\Rightarrow-2y=0\Rightarrow y=0\)
vậy x=1 thì y=1; x=0 thì y=0
x - 2xy + y = 0
<=> 2x - 4xy + 2y = 0
<=> 2x - 4xy + 2y - 1 = -1
<=> (2x - 4xy) - (1 - 2y) = -1
<=> 2x(1 - 2y) - (1 - 2y) = -1
<=> (2x - 1)(1 - 2y) = - 1
<=> 2x - 1 = -1 và 1 - 2y = 1
hoặc 2x - 1 = 1 và 1 - 2y = -1
<=>2x=2 và 2y=2
<=>x=1 và y=1

Ta có: 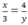 ⇔ x.y = 3.4 ⇒ x.y = 12
⇔ x.y = 3.4 ⇒ x.y = 12
Và 12 = 1. 12 = (-1).(-12) = 2.6 = (-2).(-6) = 3.4 = (-3).(-4)
Ta lần lượt có các giá trị của x, y như sau:
x = 12 ⇒ y = 1 x = -1 ⇒ y = -12
x = 6 ⇒ y = 2 x = -2 ⇒ y = -6
x = 4 ⇒ y = 3 x = -3 ⇒ y = -4
x = 3 ⇒ y = 4 x = -4 ⇒ y = -3
x = 2 ⇒ y = 6 x = -6 ⇒ y = -2
x = 1 ⇒ y = 12 x = -12 ⇒ y = -1

2xy+6x=y−22xy+6x=y−2
⇔2x(y+3)=y+3−5⇔2x(y+3)=y+3−5
⇔(2x−1)(y+3)=−5⇔(2x−1)(y+3)=−5
Xet U(-5) nhé bạn

Giải:
b) \(\left(2x+1\right).\left(y-3\right)=10\)
\(\Rightarrow\left(2x+1\right)\) và \(\left(y-3\right)\inƯ\left(10\right)=\left\{1;2;5;10\right\}\)
Vì \(\left(2x+1\right)\) là số lẻ nên \(\left(2x+1\right)\in\left\{1;5\right\}\)
Ta có bảng giá trị:
| 2x+1 | 1 | 5 |
| y-3 | 5 | 1 |
| x | 1 | 2 |
| y | 8 | 4 |
Vậy \(\left(x;y\right)=\left\{\left(1;8\right);\left(2;4\right)\right\}\)
c) \(2xy-x+2y=13\)
\(\Rightarrow x.\left(2y-1\right)+\left(2y-1\right)=12\)
\(\Rightarrow\left(x+1\right).\left(2y-1\right)=12\)
\(\Rightarrow\left(x+1\right)\) và \(\left(2y-1\right)\inƯ\left(12\right)=\left\{1;2;3;4;6;12\right\}\)
Vì \(\left(2y-1\right)\) là số lẻ nên \(\left(2y-1\right)\in\left\{1;3\right\}\)
Ta có bảng giá trị:
| x+1 | 12 | 4 |
| 2y-1 | 1 | 3 |
| x | 11 | 3 |
| y | 1 | 2 |
Vậy \(\left(x;y\right)=\left\{\left(11;1\right);\left(3;2\right)\right\}\)
Giải: (tiếp)
d) \(6xy-9x-4y+5=0\)
\(\Rightarrow3x.\left(2y-3\right)-4y=-5\)
\(\Rightarrow3x.\left(2y-3\right)-4y+6=1\)
\(\Rightarrow3x.\left(2y-3\right)-2.\left(2y-3\right)=1\)
\(\Rightarrow\left(3x-2\right).\left(2y-3\right)=1\)
\(\Rightarrow\left(3x-2\right)\) và \(\left(2y-3\right)\inƯ\left(1\right)=\left\{1\right\}\)
Ta có bảng giá trị:
| 3x-2 | 1 |
| 2y-3 | 1 |
| x | 1 |
| y | 2 |
Vậy \(\left(x;y\right)=\left\{\left(1;2\right)\right\}\)
e) \(2xy-6x+y=13\)
\(\Rightarrow2x.\left(y-3\right)+\left(y-3\right)=10\)
\(\Rightarrow\left(2x+1\right).\left(y-3\right)=10\)
Còn lại câu e nó giống hệt câu b nha nên câu lm giống nó là đc!
f) \(2xy-5x+2y=148\)
\(\Rightarrow2y.\left(x+1\right)-5x-5=143\)
\(\Rightarrow2y.\left(x+1\right)-5.\left(x+1\right)=143\)
\(\Rightarrow\left(x+1\right).\left(2y-5\right)=143\)
\(\Rightarrow\left(x+1\right)\) và \(\left(2y-5\right)\inƯ\left(143\right)=\left\{1;11;13;143\right\}\)
Ta có bảng giá trị:
| x+1 | 1 | 11 | 13 | 143 |
| 2y-5 | 143 | 13 | 11 | 1 |
| x | 0 | 10 | 12 | 142 |
| y | 74 | 9 | 8 | 3 |
Vậy \(\left(x;y\right)=\left\{\left(0;74\right);\left(10;9\right);\left(12;8\right);\left(142;3\right)\right\}\)
Chúc bạn học tốt! (Trời mk mất gần 1 tiếng bài này! ![]() )
)

2\(xy\) + \(x\) - 4\(y\) = 8 ⇔ (2\(xy\) - 4\(y\)) + \(x\) = 8 ⇔ 2\(y\)(\(x\) - 2) = 8 - \(x\)
\(y\) = (8 - \(x\)) : { 2(\(x-2\))} ⇔ \(y\) = \(\dfrac{8-x}{2\left(x-2\right)}\) (đk \(x\) \(\ne\) 2)
\(y\) \(\in\) Z ⇔ 8 - \(x\) \(⋮\) 2 (\(x-2\)) ⇔ 2 \(\times\)(8-\(x\)) ⋮ 2(\(x-2\)) ⇔ 16 - 2\(x\) ⋮ 2\(x\) - 4
⇔ -( 2\(x\) - 4) + 12 ⋮ 2\(x\) - 4 ⇔ 12 ⋮ 2\(x\) - 4
Ư(12) = { -12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
Lập bảng ta có:
⇒ \(x\) \(\in\) { -4; -1; 0; 1; 3; 4; 5; 8}
Thay \(x\) \(\in\) { - 4; -1; 0; 1; 3; 4; 5; 8} vào biểu thức \(y\) = \(\dfrac{8-x}{2x-4}\)
Ta có \(y\) \(\in\) { -1; -\(\dfrac{3}{2}\); -2; - \(\dfrac{7}{2}\); \(\dfrac{5}{2}\); 1; \(\dfrac{1}{2}\); 0}
Vậy các cặp (\(x\); y) thỏa mãn đề bài lần lượt là:
(\(x\); y) = (-4; -1); (0; -2); ( 4; 1); (8; 0)
\(2xy+x-4y=8\)
\(x\left(2y+1\right)-4y=8\)
\(x\left(2y+1\right)-4y-2=8-2\)
\(x\left(2y+1\right)-2\left(2y+1\right)=6\)
\(\left(2y+1\right)\left(x-2\right)=6\)
\(\Rightarrow2y+1\) và \(x-2\) là ước của 6
mà 2y + 1 la số lẻ nên \(2y+1\in\left(6\right)=\left\{1;3;-1;-3\right\}\)
Ta có bảng sau:
2y+1
1
3
-1
-3
x-2
6
2
-6
-2
y
0
1
-1
-2
x
8
4
-4
0
Vậy ta có 4 cặp số (x,y) thoả mãn đề bài là (8,0);(4,1);(-4,-1);(0,-2)
Chúc bạn học tốt