CSC có bao nhiêu số hạng biết: u1 = 7, un = 262 và un-1 + un = 519
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Ta có:
$u_n=9-5n; u_{n+1}=9-5(n+1)$
$\Rightarrow u_{n+1}-u_n=-5$ là hằng số
Do đó $(u_n)$ là cấp số cộng với công sai $d=-5$
$u_1=9-5.1=4$
Giả sử $-9991$ là số hạng của scs nói trên.
Khi đó:
$-9991=u_k=9-5k\Rightarrow k=2000$
$\Rightarrow -9991$ là số hạng thứ $2000$
Còn $2016$ hiển nhiên không phải số hạng của csc vì $u_n=9-5n\leq 4$ với mọi $n\in\mathbb{N}\geq 1$

u1=-1
u2=-1+3=2
u3=2+3=5
u4=5+3=8
u5=8+3=11
Công thức tổng quát là: \(U_n=U_1+\left(n-1\right)\cdot\left(3\right)=-1+3n-3=3n-4\)

1/ \(u_{16}=u_1+\left(16-1\right).d=93\)
2/ \(u_{31}=u_1+\left(31-1\right)d=-\frac{35}{2}\)

Đặt \(u_n=v_n+1\Rightarrow v_{n+1}+1=\dfrac{2017+v_n+1}{2019-\left(v_n+1\right)}=\dfrac{2018+v_n}{2018-v_n}\)
\(\Rightarrow v_{n+1}=\dfrac{2018+v_n}{2018-v_n}-1=\dfrac{2v_n}{2018-v_n}\Rightarrow\dfrac{1}{v_{n+1}}=1009\dfrac{1}{v_n}-\dfrac{1}{2}\)
Đặt \(\dfrac{1}{v_n}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{1}{v_1}=\dfrac{1}{u_1-1}=1\\x_{n+1}=1009x_n-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x_{n+1}-\dfrac{1}{2016}=1009\left(x_n-\dfrac{1}{2016}\right)\)
\(\Rightarrow x_n-\dfrac{1}{2016}\) là CSN với công bội 1009 \(\Rightarrow x_n-\dfrac{1}{2016}=\dfrac{2015}{2016}.1009^{n-1}\)
\(\Rightarrow x_n=\dfrac{2015}{2016}1009^{n-1}+\dfrac{1}{2016}\)
\(\Rightarrow u_n=v_n+1=\dfrac{1}{x_n}+1=\dfrac{2016}{2015.1009^{n-1}+1}+1\)
\(\Rightarrow\lim\left(u_n\right)=1\)
Có thể đặt \(u_n=v_n+2017\) nữa bác nhỉ, bác có công thức tổng quát tìm t không ạ: \(u_n=v_n+t\).

a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.

Đáp án B
u 2 = u 1 + 1 ; u 3 = u 2 + 3 = u 1 + 1 + 3 ; u 4 = u 3 + 5 = u 1 + 1 + 3 + 5 ; ... ; u 50 = u 1 + 1 + 3 + 5 + ... + 2.49 − 1 = 1 + 1 + 3 + 5 + ... + 97 = 1 + 1 + 97 .49 2 = 2402

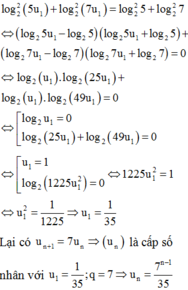
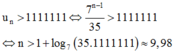
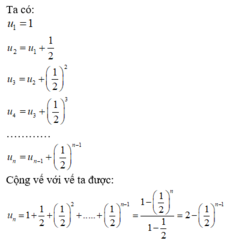
=>u1+(n-1)*d=262 và u1+(n-2)*d+u1+(n-1)*d=519
=>(n-1)*d=255 và d(n-2+n-1)=505
=>(n-1)/(2n-3)=51/101
=>101n-101=102n-153
=>-n=-52
=>n=52