Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Năm số hạng đầu của dãy số là -1, 2, 5, 8, 11.
b) Chứng minh un = 3n - 4 bằng phương pháp quy nạp:
Với n =1 thì u1 3.1 - 4 = -1, đúng.
Giả sử hệ thức đúng với n = k ≥ 1, tức là uk = 3k -4. Ta chứng minh hệ thức cũng đúng với n = k + 1.
Thật vậy, theo công thức của dãy số và giả thiết quy nạp, ta có:
uk+1 = uk + 3 = 3k - 4 + 3 = 3(k + 1) - 4.
Vậy hệ thức đúng với mọi n ε N*

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

a) Năm số hạng đầu của dãy số là 3, √10, √11, √12, √13.
b) Ta có: u1 = 3 = √9 = √(1 + 8)
u2 = √10 = √(2 + 8)
u3 = √11 = √(3 + 8)
u4 = √12 = √(4 + 8)
...........
Từ trên ta dự đoán un = √(n + 8), với n ε N* (1)
Chứng minh công thức (1) bằng phương pháp quy nạp:
- Với n = 1, rõ ràng công thức (1) là đúng.
- Giả sử (1) đúng với n = k ≥ 1, tức là có uk = √(k + 8) với k ≥ 1.
Theo công thức dãy số, ta có:
uk+1 = .
Như vậy công thức (1) đúng với n = k + 1.

Đề bài không rõ ràng. n ở đây là tự nhiên, nguyên hay là chơi luôn cả R

a. Năm số hạng đầu của dãy số
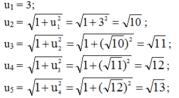
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
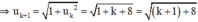
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

a) Ta có:
u1 = 2, u2 = 2u1 – 1 = 3, u3 = 2u2 – 1= 5
u4 = 2u3 -1 = 9, u5 = 2u4 – 1= 10
b) Với n = 1, ta có: u1 = 21-1 + 1 = 2 : đúng
Giả sử công thức đúng với n = k. Nghĩa là: uk = 2k-1 + 1
Ta chứng minh công thức cũng đúng với n = k + 1,
Nghĩa là chứng minh:
Uk+1 = 2(k+1)-1 + 1 = 2k + 1
Ta có: uk+ 1 = 2uk – 1 = 2(2k -1+ 1) -1 = 2.2k -1 + 2 – 1 = 2k + 1 (đpcm)
Vậy un = 2n-1 + 1 với mọi n ∈ N*
a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3(k+1) - 4
Thật vậy,ta có : uk + 1 = uk + 3 = 3k – 4 + 3 = 3(k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.