Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B đối xứng với A qua O ⇒ O là trung điểm của AB
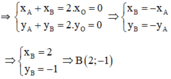
C có tung độ bằng 2 nên C(x; 2)
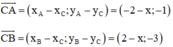
Tam giác ABC vuông tại C
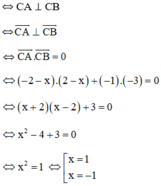
Vậy có hai điểm C thỏa mãn là C1(1; 2) và C2(–1; 2).

Chắc là A,B,M thẳng hàng chứ?
Do M thuộc Oy nên tọa độ có dạng: \(M\left(0;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BA}=\left(2;5\right)\\\overrightarrow{BM}=\left(1;m+2\right)\end{matrix}\right.\)
A, B, M thẳng hàng \(\Rightarrow\overrightarrow{BA}\) cùng phương \(\overrightarrow{BM}\)
\(\Rightarrow\dfrac{1}{2}=\dfrac{m+2}{5}\Rightarrow m=\dfrac{1}{2}\)
\(\Rightarrow M\left(0;\dfrac{1}{2}\right)\)

Do A(2; 4) nên A cách trục Ox 2 đơn vị, cách trục Oy 4 đơn vị
Khi đó đường tròn (A; 2) tiếp xúc với trục Ox và không giao nhau với trục Oy

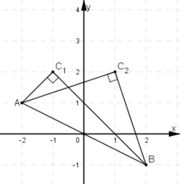
Điểm B đối xứng với A qua gốc tọa độ nên tọa độ của B là (2; -1)
Tọa độ của C là (x; 2). Ta có: = (-2 – x; -1)
= (-2 – x; -3)
Tam giác ABC vuông tại C => ⊥
=>
.
= 0
=> (-2 – x)(2 – x) + (-1)(-3) = 0
=> -4 + x2+ 3 = 0
=> x2 = 1 => x= 1 hoặc x= -1
Ta được hai điểm C1(1; 2); C2(-1; 2)
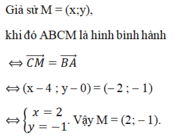
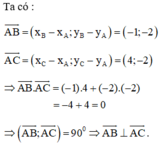
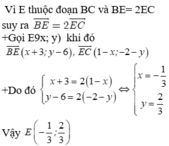
a: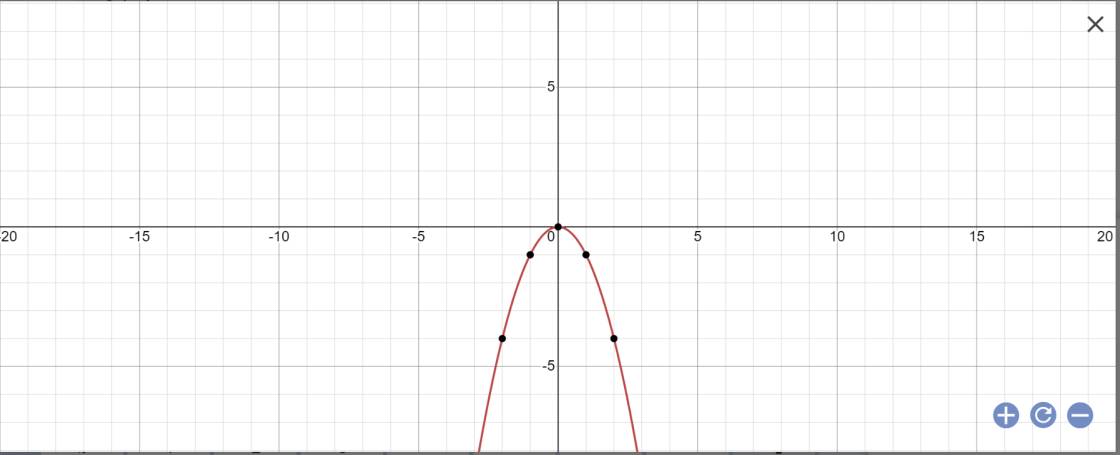
b: Phương trình OA có dạng là y=ax+b
Theo đề, ta có hệ:
0a+b=0 và a+b=1
=>b=0 và a=1
=>y=x
Vì (d)//OA nên (d): y=x+b
Thay x=2 và y=0 vào (d), ta được:
b+2=0
=>b=-2
=>y=x-2
PTHĐGĐ là:
-x^2-x+2=0
vì a*c<0
nên (P) luôn cắt (d) tại hai điểm phân biệt