Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. SO vuông góc (ABCD) và \(SO=\dfrac{a\sqrt{3}}{2}\). Tính \(\widehat{\left(SBC\right);\left(ABCD\right)}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\)
\(tan\widehat{SCO}=\dfrac{SO}{OC}=\sqrt{3}\Rightarrow\widehat{SCO}=60^0\)
c.
Gọi E là trung điểm CD, từ O kẻ \(OF\perp SE\)
OE là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=a\\OE||BC\Rightarrow OE\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SOE\right)\)\(\Rightarrow CD\perp OF\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Do \(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF\)
Hệ thức lượng: \(OF=\dfrac{OE.SO}{\sqrt{OE^2+SO^2}}=...\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
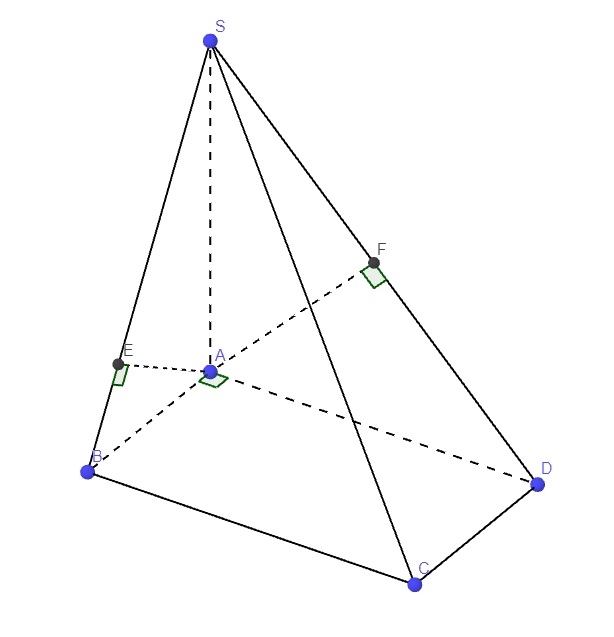
Lần lượt kẻ \(AE\perp SB\) (1) và \(AF\perp SD\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AE\) (2)
(1);(2) \(\Rightarrow AE\perp\left(SBC\right)\)
Hoàn toàn tương tự ta có \(AF\perp\left(SCD\right)\)
\(\Rightarrow\) Góc giữa (SBC) và (SCD) là góc giữa AE và AF
Cũng từ \(BC\perp\left(SAB\right)\) mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBCD) và đáy
\(\Rightarrow\widehat{SBA}=60^0\Rightarrow SA=AB.tan60^0=a\sqrt{3}\)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(\dfrac{1}{AF^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AF=\dfrac{a\sqrt{6}}{2}\)
\(SB=\sqrt{SA^2+AB^2}=2a\) ; \(SD=a\sqrt{6}\)
\(BD=\sqrt{AB^2+AD^2}=2a\Rightarrow cos\widehat{BSD}=\dfrac{SB^2+SD^2-BD^2}{2SB.SD}=\dfrac{\sqrt{6}}{4}\)
\(SE=\sqrt{SA^2-AE^2}=\dfrac{3a}{2}\) ; \(SF=\sqrt{SA^2-AF^2}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow EF=\sqrt{SE^2+SF^2-2SE.SF.cos\widehat{BSD}}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow cos\widehat{EAF}=\dfrac{AE^2+AF^2-EF^2}{2AE.AF}=\dfrac{\sqrt{2}}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(AC=2OA=2a\sqrt{2}\) \(\Rightarrow AB=\dfrac{AC}{\sqrt{2}}=2a\)
Gọi M là trung điểm BC \(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy
\(OM=\dfrac{1}{2}AB=a\)
\(\Rightarrow tan\widehat{SMO}=\dfrac{SO}{OM}=\sqrt{3}\Rightarrow\widehat{SMO}=60^0\)
MH
17 tháng 4 2022
Do S.ABCD có đáy là hình vuông và \(SO\perp\left(ABCD\right)\) nên nó là hình chóp tứ giác đều, do đó các cạnh bên bằng nhau và các mặt bên tạo với đáy các góc bằng nhau.
Gọi \(H\) là trung điểm \(AB\).
Ta có \(\left\{{}\begin{matrix}\left(SAB\right)\cap\left(ABCD\right)=AB\\OH\perp AB\\SH\perp AB\end{matrix}\right.\Rightarrow\left(\left(SAB\right);\left(ABCD\right)\right)=\left(OH,SH\right)=\widehat{SHO}\)
Ta có \(OA=a\sqrt{2}\Rightarrow AC=2.OA=2a\sqrt{2}\Rightarrow AB=AD=2a\)
\(\Rightarrow OH=\dfrac{1}{2}AD=a\)
Trong tam giác SHO, ta có: \(tan\widehat{SHO}=\dfrac{SO}{OH}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\Rightarrow\widehat{SHO}=60^0\)
Đáp án C
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2023
B là khẳng định sai
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
\(CD=\left(SCD\right)\cap\left(BCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SDC) và (BCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{2}\Rightarrow\widehat{SDA}\approx54^044'\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2021
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 4 2023
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà CD là giao tuyến (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=60^0\Rightarrow SA=AD.tan60^0=3a\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}=...\)
b.
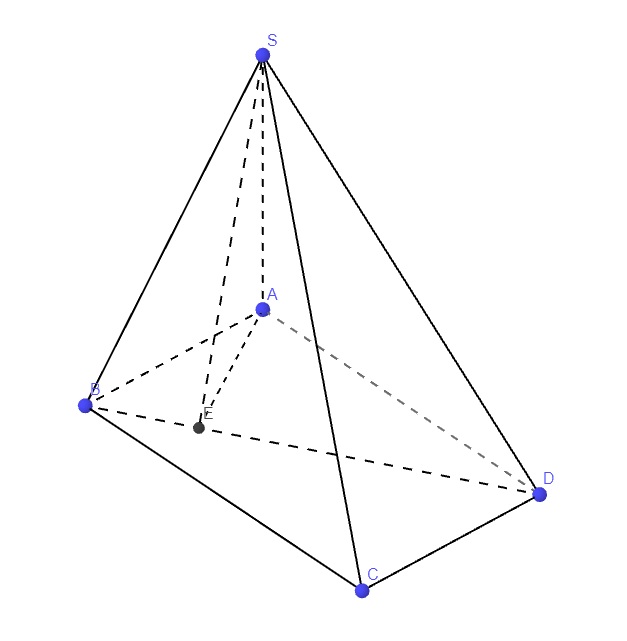
Từ A kẻ \(AE\perp BD\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\)
\(\Rightarrow BD\perp\left(SAE\right)\Rightarrow\widehat{SEA}\) là góc giữa (SBD) và (ABCD)
Hệ thức lượng: \(\dfrac{1}{AE^2}=\dfrac{1}{AB^2}+\dfrac{1}{AD^2}\Rightarrow AE=\dfrac{a\sqrt{3}}{2}\)
\(tan\widehat{SEA}=\dfrac{SA}{AE}=2\sqrt{3}\Rightarrow\widehat{SEA}=...\)
CM
7 tháng 4 2019
Đáp án C
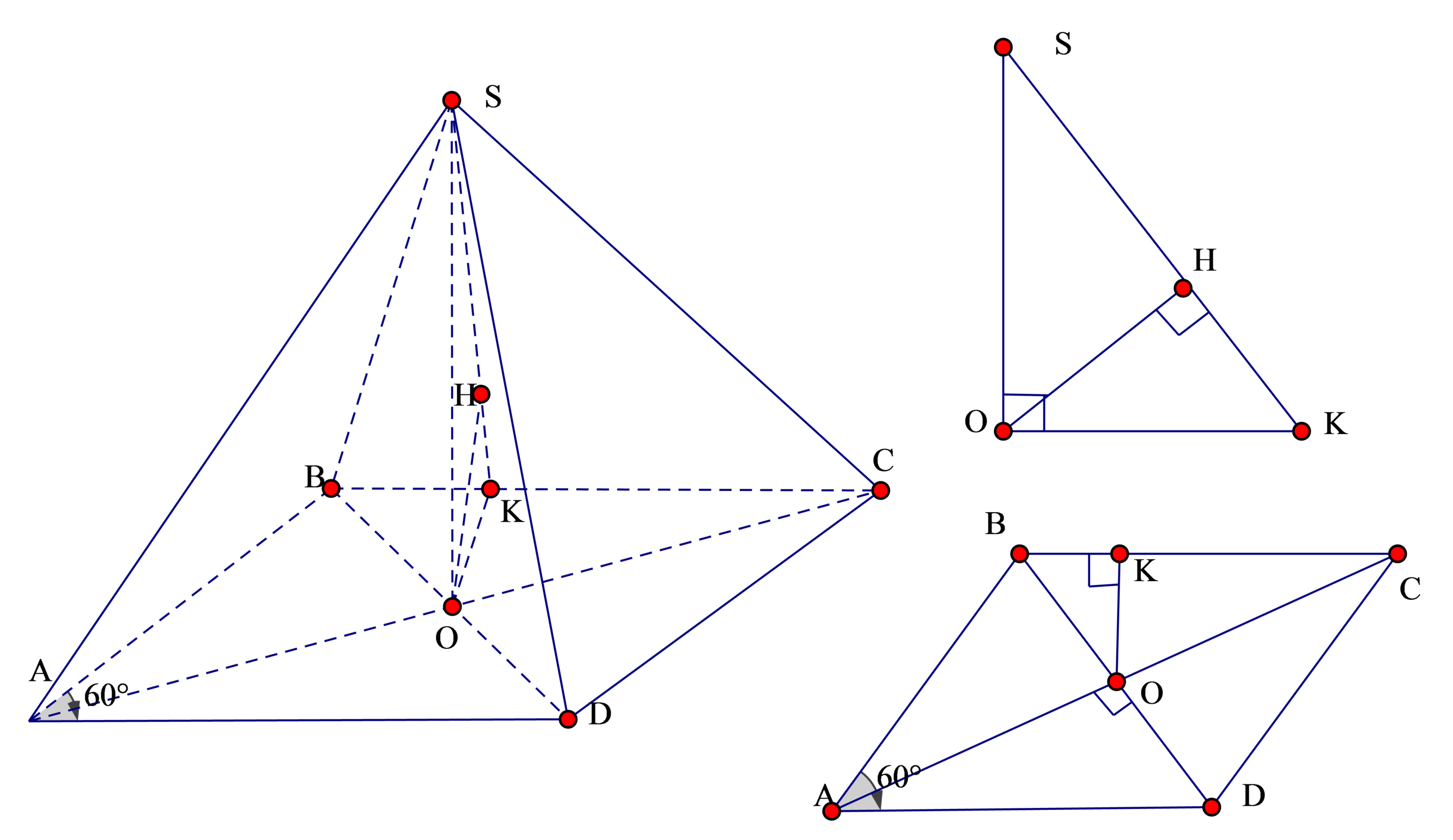
Kẻ O K ⊥ B C , O H ⊥ S K như hình vẽ khi đó OH là khoảng cách từ O tới (SBC)
Dễ thấy Δ A B D đều
⇒ O K = O B . sin 60 0 = a 2 . 3 2 = a 3 4
Ta có: 1 O H 2 = 1 O K 2 + 1 S O 2 = 16 3 a 2 + 1 a 2 = 19 3 a 2
⇒ O H = a 57 19
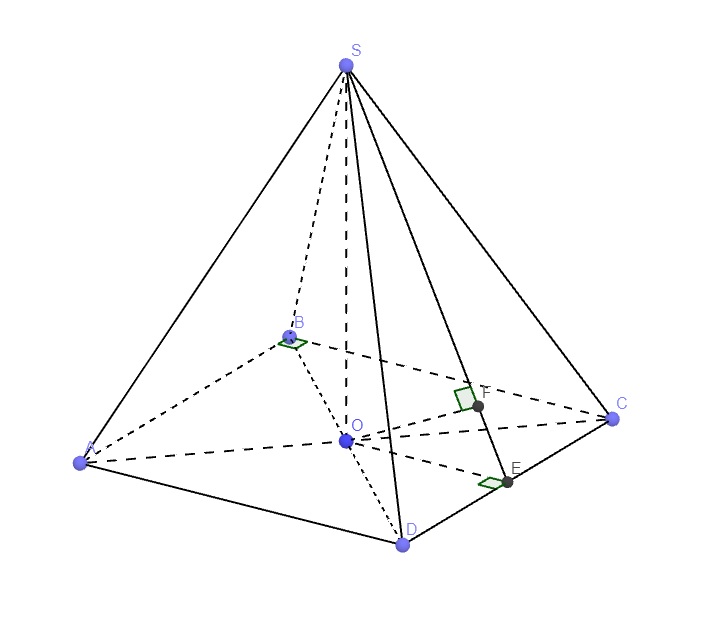
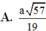
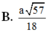
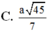
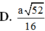
Gọi E là trung điểm BC \(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}AB=\dfrac{a}{2}\\OE||AB\Rightarrow OE\perp BC\end{matrix}\right.\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SEO\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\Rightarrow\widehat{SEO}=60^0\)