vẽ tam gíac mnp biết mnp=4 cm, mp= 5cm,np=7 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bước 1: Vẽ NP = 7cm
Bước 2: Tại điểm N vẽ cung tròn tâm N bán kính MN = 4cm
Tại điểm P vẽ cung tròn tâm P bán kính MP = 5cm
2 cung tròn này cắt nhau ở đâu thì đó là điểm M
Bước 3: Nối MN, MP ta được tam giác MNP
Cứ làm theo 3 bước trên ta vẽ được tam giác MNP

Sửa đề: MN-NP=3cm
ΔABC=ΔMNP
=>AB=MN; BC=NP; AC=MP
MN-NP=3
=>AB-BC=3
mà AB+BC=7
nên \(AB=\dfrac{3+7}{2}=5cm;BC=AB-3=5-3=2cm\)
MP=AC
mà MP=4cm
nên AC=4cm
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=5+4+2=11\left(cm\right)\)
Chu vi tam giác MNP là:
\(C_{MNP}=MN+NP+MP=5+4+2=11\left(cm\right)\)

tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)


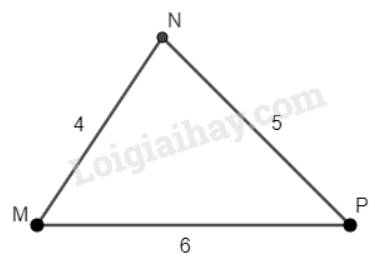
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)

Bạn tự vẽ hình nhá :v
a) Ta có : MP - NP < MN < MP + NP
=> 6 < MN < 8
Vì độ dài của đoạn MN là số nguyên nên : MN = 7 ( cm )
b) MN = NP = 7 ( cm )
Nên \(\Delta MNP\) là tam giác cân tại M.
a) Ta có:
MP−NP<MN<MP+NP
⇒6<MN<8⇒6<MN<8
Vì độ dài MNMN là số nguyên nên:
MN=7(cm)MN=7(cm)
b) MN=NP=7(cm)MN=NP=7(cm)
Nên MNPMNP là tam giác cân tại M

Chứng minh tam giác vuông mà thấy số liệu là mừng chết mất =)))
Xét tam giác MNP có:
\(MN^2=NP^2+MP^2\)
\(10^2=6^2+8^2\)
\(100=36+64\)
Vậy trong tam giác này sử dụng được pytago
=> Tam giác MNP vuông tại P
Hình dễ lắm b. Lúc này hình chưa chứng minh là vuông nhé :)
P N M
Bây giờ mới để ý chỗ đề viết sai. Tam giác MNP chứ lấy đâu ra R? :)