Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

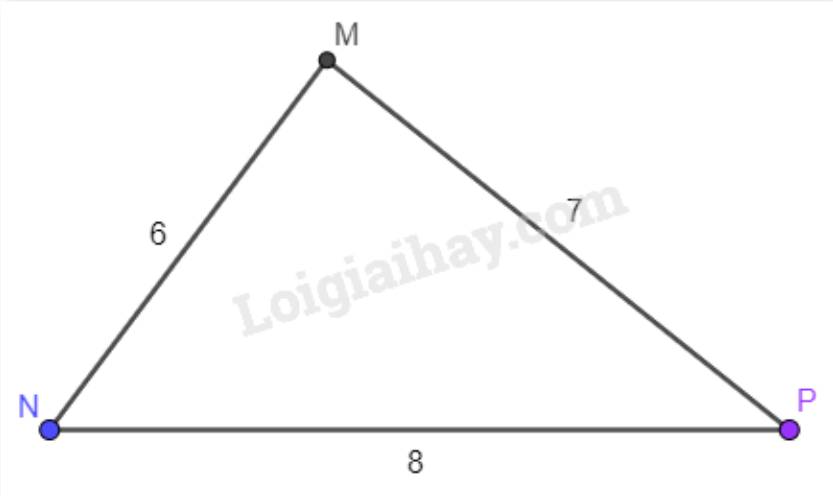
Trong tam giác MNP ta có: \(MN < MP < NP\) (6 < 7 < 8).
Vậy góc lớn nhất trong tam giác MNP là góc M (đối diện với cạnh NP) và góc nhỏ nhất trong tam giác MNP là góc P (đối diện với cạnh MN).

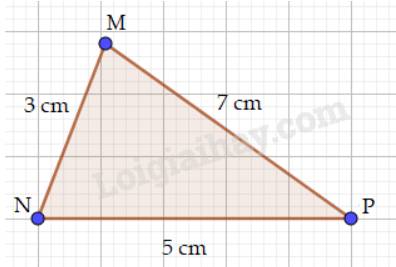
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

đề 2 :
MN = 6 cm, MP= 8 cm , NP= 10 cm
ta có : mn^2 + mp^2=6^2+8^2=100
np^2=100
suy ra mp^2+mn^2=np^2
vậy tam giác mnp vuông tại M
kick mk nha
đề 1: vì tổng 3 góc trong 1 tam giác là 180*
mà tam giác abc cân tại a suy ra : góc b = góc c
góc b +góc c=180-80=100
vì góc b = góc c suy ra :
góc b = góc c = 50 *

a) Từ \(\Delta ABC\)cân tại A, \(\Rightarrow\widehat{B}=\widehat{C}=75^o\)
\(\Rightarrow\widehat{A}=180^o-\left(\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{A}=180^o-\left(75^o+75^o\right)\)
\(\Rightarrow\widehat{A}=30^o\)
b) Từ \(\Delta MNP\)cân tại P, \(\Rightarrow\widehat{M}=\widehat{N}=\frac{180^o-\widehat{P}}{2}=\frac{80^o}{2}=40^o\)
c) Ta có: \(NP^2=13^2=169\)(1)
\(MN^2+MP^2=5^2+12^2=25+144=169\)(2)
Từ (1) và (2) suy ra: \(NP^2=MN^2+MP^2\)
\(\Rightarrow\Delta MNP\)vuông (theo định lí Pytago)
Happy new year!!!
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)