Tìm hệ số của x4 trong khai triển của (3x –1)^5. A.-90 B.90 C.820 D.830
Giúp vs e
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có : \(\left(1-3x\right)^n=\sum\limits^n_{k=0}C^k_n\left(1\right)^{n-k}\left(-3\right)^k\left(x^k\right)\)
để có \(x^2\) trong khai triển thì \(k=2\)
khi đó hệ số của số hạng chứa \(x^2\) là \(\)\(C^2_n\left(-3\right)^2=90\)
\(\Leftrightarrow C^2_n=10\Leftrightarrow\dfrac{n!}{2!\left(n-2\right)!}=10\) \(\Leftrightarrow\dfrac{n\left(n-1\right)}{2}=10\)
\(\Leftrightarrow n^2-n-20=0\left[{}\begin{matrix}n=5\left(N\right)\\n=-4\left(L\right)\end{matrix}\right.\) vậy \(n=5\)

+ Số hạng tổng quát của khai triển (1 – 3x)n là:
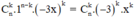
+ Số hạng chứa x2 ứng với k = 2.
Hệ số của x2 là 90 nên ta có:
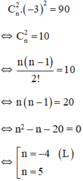
Vậy n = 5.

Chọn B.
(
2
+
3
x
)
5
có công thức số hạng tổng quát là: ![]() .
.
Với k = 4, ta được số hạng ![]() .
.
Vậy hệ số của số hạng chứa x 4 trong khai triển ( 2 + 3 x ) 5 là 810.

|
Với số thực x ≠ 0 và với mọi số tự nhiên n ≥ 1, ta có: (1 - 3x)n = [1 - (3x)]n = Suy ra hệ số của x2trong khai triển này là 32C2n .Theo giả thiết, ta có: 32C2n = 90 => C2n = 10. Từ đó ta có:
⇔ n2 – n – 20 = 0 ⇔ n = -4 (loại) hoặc n = 5. ĐS: n = 5. |

Hệ số của x^4 sẽ là tổng của 2*a và 1*b, với a là hệ số của x^3 trong (x-1)^5, b là hệ số của x^4 trong (x-1)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot\left(-1\right)^k\cdot x^{5-k}\)
Số hạng chứa x^3 tương ứng với 5-k=3
=>k=2
=>Hệ số là \(C^2_5\cdot\left(-1\right)^2=10\)
Số hạng chứa x^4 tương ứng với 5-k=4
=>k=1
=>Hệ số là \(C^1_5\cdot\left(-1\right)=-5\)
=>Hệ số của x^4 là: 2*10+1*(-5)=20-5=15
Ta có:
\(\left(3x-1\right)^5\)\(=\sum\limits^5_{k=0}.\left(-1\right)^k.C^k_5.\left(3x\right)^{5-k}.1^k\)
\(=\sum\limits^5_{k=0}.\left(-1\right)^k.C^k_5.3^{5-k}.x^{5-k}.1\)
Để số hạng tổng quát có chứa \(x^4\) thì \(5-k=4\Rightarrow k=1\)
Vậy hệ số của \(x^4\) là: \(\left(-1\right)^1.C^1_5.3^{5-1}.1=-405\)
→ Không có đáp án