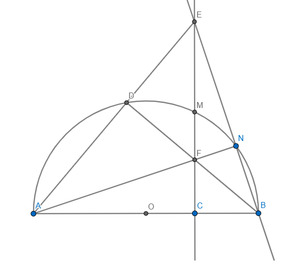
Cho nửa đường tròn (O) đường kính AB và đường thẳng d vuông góc với AB tại H ( H thuộc đoạn OA ), M là một điểm di động trên nửa đường tròn khác phía với A bởi đường thẳng d. Đường thẳng d cắt MA, MB lần lượt lại C và D
1) Chứng minh tứ giác BHCM nội tiếp
2) Chứng minh HC.HD = HA.HB
3) Gọi K là điểm dối xứng của B qua H. Chứng minh tứ giác ACDK nội tiếp
4) Khi M chạy trên nửa đường tròn thì tâm đường tròn ngoại tiếp tam giác ADC chạy trên đường nào?


1: góc BHC+góc BMC=180 độ
=>BHCM nội tiếp
2: Xet ΔHDB vuông tại H và ΔHAC vuông tại H có
góc HAC=góc HDB
=>ΔHDB đồng dạng với ΔHAC
=>HD/HA=HB/HC
=>HD*HC=HA*HB