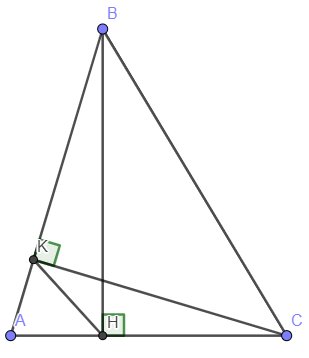
Cho tam giác ABC. BH, CK là đường cao tam giác ABC. HE, KF là đường cao tam giác AHK. chứng minh rằng EF//BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


△AKC∼△AHB (g-g) \(\Rightarrow\dfrac{CK}{BH}=\dfrac{AC}{AB}\Rightarrow\dfrac{CK}{BH}=\dfrac{AC}{AB}=\dfrac{AC-CK}{AB-BH}=1\)
\(\Rightarrow AB=AC\Rightarrow\)△ABC cân tại A.
\(AB\ge BH\Rightarrow AB+CK\ge BH+CK\Rightarrow AC+BH\ge BH+CK\Rightarrow AC\ge CK\)-Dấu bằng xảy ra khi và chỉ khi \(A\equiv H\Leftrightarrow\)△ABC vuông tại A.

Câu hỏi của duyvodich10 - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

Câu hỏi của duyvodich10 - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

a: Xét ΔACI vuông tại C và ΔAHB vuông tại H có
góc CAI=góc HAB
=>ΔACI đồng dạng với ΔAHB
b: Xét ΔHBI và ΔHAB có
góc HBI=góc HAB
góc H chung
=>ΔHBI đồng dạng với ΔHAB
=>HB/HA=HI/HB
=>HB^2=HA*HI
c: CD/DA=CK/KA=CB/CA
a.
Xét hai tam giác AIC và ABH có:
\(\left\{{}\begin{matrix}\widehat{CAI}=\widehat{BAH}\left(\text{Ax là phân giác}\right)\\\widehat{ACI}=\widehat{AHB}=90^0\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AIC\sim\Delta ABH\left(g.g\right)\) (1)
b.
Xét hai tam giác AIC và BIH có:
\(\left\{{}\begin{matrix}\widehat{AIC}=\widehat{BIH}\left(\text{đối đỉnh}\right)\\\widehat{ACI}=\widehat{BHI}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AIC\sim\Delta BIH\left(g.g\right)\) (2)
(1);(2) \(\Rightarrow\Delta ABH\sim\Delta BIH\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{BH}{IH}\Rightarrow BH^2=HI.HA\)
c.
Áp dụng định lý phân giác trong tam giác ACK: \(\dfrac{CD}{DA}=\dfrac{CK}{AK}\) (3)
Xét hai tam giác ABC và ACK có:
\(\left\{{}\begin{matrix}\widehat{CAB}\text{ chung}\\\widehat{BCA}=\widehat{CKA}=90^0\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABC\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{BC}{CK}=\dfrac{AC}{AK}\Rightarrow\dfrac{BC}{AC}=\dfrac{CK}{AK}\) (4)
(3);(4) \(\Rightarrow\dfrac{CD}{DA}=\dfrac{BC}{AC}\)

Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
góc A chung
=>ΔAHB đồng dạng với ΔAKC
=>AH/AK=AB/AC
=>AH/AB=AK/AC
Vì góc BKC=góc BHC=90 độ
nên BKHC nội tiếp
=>góc AKH=góc ACB
góc KEH=góc KFH=90 độ
nên KEFH nội tiếp
=>góc AEF=góc AHK=góc ABC
=>EF//CB
cai nay lop 7 thi phai lam cach lop 7 chu