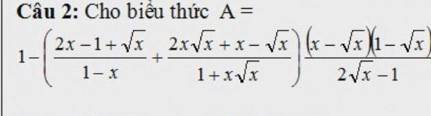
Giúp mik rút gọn bài này vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MV
3
17 tháng 2 2016
a. (a+b).(a+b)
= a+b.a+b
= (a+b)2
b, (a-b).(a-b)
= a-b.a-b
= (a-b)2
17 tháng 2 2016
a,(a+b).(a+b)
=(a+b).a+(a+b).b
=a2+ba+ab+b2
=(a2+b2)+2ab
b,(a-b).(a-b)
=(a-b).a-(a-b).b
=a2-ba-ab-b2
=(a2-b2)-(ab-ba)
=a2-b2
UT
14 tháng 2 2022
Tham khảo e nhé!
Tiếng trống trường vang lên rộn rã, báo hiệu giờ ra chơi của chúng em đã đế. Sân trường đang lặng thinh, im ắng bỗng trở nên rộn rã bởi tiếng cười, tiếng nói của các cô cậu học trò. Góc ghế đá sân trường, các bạn nữ ngồi thầm thì nhỏ to với những câu chuyện vui vẻ. Rất nhiều bạn học sinh khác chọn không gian ở căng tin canh sân trường để tranh thủ ăn sáng hoặc cùng ngồi uống nước, nghỉ ngơi sau giờ học căng thẳng. Rộn ràng nhất là góc sân trường, mọi người đang tổ chức rất nhiều trò chơi vui nhộn. Nhảy dây. Kéo co. Chơi bóng rổ. Tất cả tạo nên một bức tranh nhộn nhịp, vui tươi về giờ ra chơi dưới sân trường.
Câu rút gọn: Nhảy dây. Kéo co. Chơi bóng rổ.
VN
19 tháng 3 2017
\(3\sqrt{8}-\sqrt{50}-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=6\sqrt{2}-5\sqrt{2}-\left(\sqrt{2}-1\right)\)
\(=\sqrt{2}-\sqrt{2}+1\)
\(=1\)
TP
1
KC
1
HN
19 tháng 3 2022
ĐK: x\(\ne\){-3;0;3}.
\(\dfrac{x^2-3x}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{3x^2}=\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{3x^2}=\dfrac{1}{3x}\).
19 tháng 10 2020
\(P=\left(1^2+2^2+...............+2015^2\right):\left(2^2+4^2+........+4030^2\right)\)
\(P=\left(1^2+2^2+............+2015^2\right):\left[\left(1.2\right)^2+\left(2.2\right)^2+.............+\left(2.2015\right)^2\right]\)
\(P=\left(1^2+2^2+........+2015^2\right):\left(1^2.2^2+2^2.2^2+...............+2015^2.2^2\right)\)
\(P=\left(1^2+2^2+......+2015^2\right):2^2.\left(1^2+2^2+.........+2015^2\right)\)
\(P=\left(1^2+2^2+........+2015^2\right).\frac{1}{2^2.\left(1^2+2^2+..............+2015^2\right)}\)
\(P=\frac{1^2+2^2+...............+2015^2}{2^2.\left(1^2+2^2+............+2015^2\right)}=\frac{1}{2^2}=\frac{1}{4}\)
Chúc bạn học tốt
ND
1
26 tháng 8 2018
3√2 - 5√18 + 6√72 - 4√98 = 3√2-5.3√2+6.2.3√2-4.7/3.3√2
= 3√2(1-5+12-28/3)
= 3√2.(-4/3)
= -4√2
ĐKXĐ:
\(\left\{{}\begin{matrix}x\ge0\\1-x\ne0\\1+x\sqrt{x}\ne0\\2\sqrt{x}-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne1\\x\ne\dfrac{1}{4}\end{matrix}\right.\)
\(A=1-\left(\dfrac{2x-1+\sqrt{x}}{1-x}+\dfrac{2x\sqrt{x}+x-\sqrt{x}}{1+x\sqrt{x}}\right)\dfrac{\left(x-\sqrt{x}\right)\left(1-\sqrt{x}\right)}{2\sqrt{x}-1}\)
\(A=1-\left(\dfrac{\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}{\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}{\left(1+\sqrt{x}\right)\left(x-\sqrt{x}+1\right)}\right)\dfrac{\left(x-\sqrt{x}\right)\left(1-\sqrt{x}\right)}{2\sqrt{x}-1}\)
\(A=1-\left(\dfrac{1}{1-\sqrt{x}}+\dfrac{\sqrt{x}}{1-\sqrt{x}+x}\right)\left(x-\sqrt{x}\right)\left(1-\sqrt{x}\right)\)
\(A=1-\dfrac{1-\sqrt{x}+x+\sqrt{x}-x}{\left(1-\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}\left(x-\sqrt{x}\right)\left(1-\sqrt{x}\right)\)
\(A=1-\dfrac{x-\sqrt{x}}{1-\sqrt{x}+x}=\dfrac{1-\sqrt{x}+x-x+\sqrt{x}}{1-\sqrt{x}+x}=\dfrac{1}{1-\sqrt{x}+x}\)