khi rót nước từ bình sang cốc nhờ dang năng dượng nào mà nc chảy từ bình sang cốc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
7 tháng 12 2023
Quan sát ta thấy bình nước của Viết rót được 8 cốc nước, bình nước của Mai rót được 7 cốc nước.
Mà 8 > 7, do đó bình nước của Việt chứa được nhiều nước hơn.
Lượng nước ở bình của Việt nhiều hơn ở bình của Mai số cốc nước là:
8 – 7 = 1 (cốc)
Q
28 tháng 7 2021
vì tỉ lệ đổi từ kg sang l là 1:1 nên mình lấy luôn nhá
lần đổ 1 \(m\left(60-t_1\right)=10\left(t_1-20\right)\left(1\right)\)
lần đổ 2 \(m\left(59-t_1\right)=5-m\Leftrightarrow m\left(60-t_1\right)=5\left(2\right)\)
chia 2 vế 1 cho 2
\(1=2.\left(t_1-20\right)\Rightarrow t_1=20,5^oC\)
\(\Rightarrow m\approx0,126\left(kg\right)\)
HM
28 tháng 7 2021
sao lại là lần đổ 1m, lần đổ 2m
mik vẫn lm lí 9 chưa hiểu lắm, còn tỉ lệ đổi từ kg -> l là 1:1 là sao vậy bạn
16 tháng 11 2019
Người ta có thể rót khí CO 2 từ cốc này sang cốc khác là do tính chất : CO 2 là chất nặng hơn không khí
Đáp án: A
cốc. Lượng nước ở bình B là 
cốc.
cốc.
TN
8 tháng 4 2023
a/
Lượng nước ở bình A là 4 cốc. Lượng nước ở bình B là 6 cốc.
b/
Lượng nước ở bình B nhiều hơn lượng nước ở bình A là 2 cốc.
8 tháng 4 2023
a. Lượng nước ở bình A là 4 cốc. Lượng nước ở bình B là 6 cốc.
b.Lượng nước ở bình B nhiều hơn lượng nước ở bình A là 2 cốc.
7 tháng 1 2022
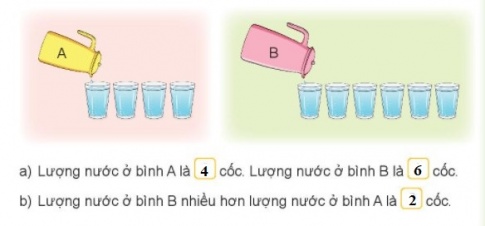
a. Nhiệt độ cân bằng ở bình 2 và lượng nước đã rót là:
\(Q_{toa}=Q_{thu}\)
\(<=> m_2c(t_2-t)=mc(t-t_1)\)
\(<=> 4(60-t)=m(t-20)\)
\(<=> m=\dfrac{4(60-t)}{t-20}(1)\)
\(Q_{toa}=Q_{thu}\)
\(<=> mc(t-t')=(m_1-m)c(t'-t_1)\)
\(<=> m(t-21,95)=(2-m)(21,95-20)\)
\(<=> m(t-21,95)=3,9-1,95 m\)
\(<=> m(t-20)=3,9=> m=\dfrac{3,9}{t-20}(2)\)
Từ \((1)(2)\) \(=> \dfrac{4(60-t)}{t-20}=\dfrac{3,9}{t-20}\)
\(<=> 240-4t=3,9\)
\(<=> 4t=236,1=> t=59,025^oC\)
\(=> m=\dfrac{3,9}{59,025-20}=0,1kg\)
b. Nếu tiếp tục thực hiện lần thứ hai nhiệt độ cân bằng ở mỗi bình là:
\(Q_{toa}=Q_{thu}\)
\(<=> m_2c(t-t_2')=mc(t_2'-t')\)
\(<=> 4(59,025-t_2')=0,1(t_2'-21,95)\)
\(<=> t_2'=58,12^oC\)
\(Q_{toa}=Q_{thu}\)
\(<=>mc(t_2'-t_1')=(m_1-m)c(t_1'-t_1)\)
\(<=>0,1(58,12-t_1')=(2-0,1)(t_1'-21,95)\)
\(<=>t_1'=23,76^oC\)
27 tháng 5 2016
- Gọi lượng nước rót mỗi lần là x ( lít); nhiệt độ cân bằng nhiệt ở bình B là t0(0C); nhiệt dung riêng của nước là c( J/kg.độ); với nước thì 1lít= 1kg
- Lần rót 1: Từ bình A sang bình B ta có phương trình cân bằng nhiệt ở bình B:
x.c.(60 – t0) = 1.c.(t0 – 20)
↔ x.(60 – t0) = (t0 – 20)
↔ x = \(\frac{t_0-20}{60-t_0}\) (1)
- Lần rót 2: Từ bình B sang bình A ta có phương trình cân bằng nhiệt ở bình A:
(5-x).c(60-59) = x.c.(59- t0)
↔ 5-x = x.(59- t0) (2)
- Từ (1;2) ta có: 5- \(\frac{1_0-20}{60-t_0}\)= \(\frac{t_0-20}{60-t_0}\).(59- t0)
↔5.(60-t0)- t0 + 20 = (t0- 20).(59-t0)
↔300- 5t0 –t0 +20 = 59.t0- t02 – 1180 +20.t0
↔t02 – 85.t0 + 1500 = 0.
Giải ra được t0 = 25 (0C) thay vào (1) được x = 1/7( lít)
Cơ năng