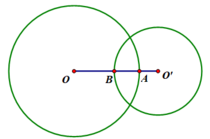
Cho 2 đường tròn (O) và (O') cắt nhau tại AB. Qua A vẽ tiếp tuyến Ax với (O) cắt (O') tại E. Qua A vẽ tiếp tuyến Ay với (O') cắt (O) tại D. Chứng minh AB^2=BD.DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

9 tháng 8 2023
a: Xét (OC/2) có
góc OMC là góc nội tiếp chắn nửa đường tròn
=>góc OMC=90 độ
=>CM vuông góc MO
Xét (O') có
góc BPC nội tiếp
BC là đường kính
=>góc BPC=90 độ
=>BP vuông góc CM
=>BP//OM

1 tháng 6 2023
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA^2=MC*MD=MH*MO
=>MC/MO=MH/MD
=>ΔMCH đồng dạng với ΔMOD
=>góc MCH=góc MOD
=>góc HOD+góc HCD=180 độ
=>HODC nội tiếp



góc AEB=góc DAB(=1/2*sđ cung AB(O'))
góc ADB=góc BAE(=1/2*sđ cung AB(O))
=>ΔABD đồng dạng với ΔEBA
=>BA/BE=BD/BA
=>BA^2=BE*BD