Tính \(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}+\sqrt{2+....}}}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2021
Sửa đề: \(\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
Ta có: \(\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{4-2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{4-2-\sqrt{3}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2-\sqrt{3}}\)
=1
3 tháng 8 2023
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{2^2-\left(2+\sqrt{2+\sqrt{3}}\right)^2}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{4-2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\cdot\sqrt{2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{4-2-\sqrt{3}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2-\sqrt{3}}=\sqrt{4-3}=1\)
13 tháng 6 2023
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\sqrt{4-2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{4-2-\sqrt{3}}\)
=1
3 tháng 8 2023
=√2+√3⋅√2+√2+√3⋅√22−(2+√2+√3)2=2+3⋅2+2+3⋅22−(2+2+3)2
=√2+√3⋅√2+√2+√3⋅√4−2−√2+√3=2+3⋅2+2+3⋅4−2−2+3
=√2+√3⋅√2+√2+√3⋅√2−√2+√3=2+3⋅2+2+3⋅2−2+3
=√2+√3⋅√4−2−√3=2+3⋅4−2−3
=√2+√3⋅√2−√3=√4−3=1
13 tháng 6 2023
\(=\sqrt{2+\sqrt{3}}\cdot\sqrt{2+\sqrt{2+\sqrt{3}}}\sqrt{2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}\sqrt{2-\sqrt{3}}=1\)
24 tháng 5 2022
e có phát hiện mới:v cj chung lớp vs cj kia đúng hemm:v
VD
25 tháng 5 2022
\(R=\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\left(\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}\right)\\ =\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{\left(2+\sqrt{2+\sqrt{2+\sqrt{3}}}\right)\left(2-\sqrt{2+\sqrt{2+\sqrt{3}}}\right)}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2^2-\left(\sqrt{2+\sqrt{2+\sqrt{3}}}\right)^2}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{4-\left(2+\sqrt{2+\sqrt{3}}\right)}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2-\sqrt{2+\sqrt{3}}}\)
\(=\sqrt{2+\sqrt{3}}.\left(\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2-\sqrt{2+\sqrt{3}}}\right)\\ =\sqrt{2+\sqrt{3}}.\sqrt{\left(2+\sqrt{2+\sqrt{3}}\right)\left(2-\sqrt{2+\sqrt{3}}\right)}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2^2-\left(\sqrt{2+\sqrt{3}}\right)^2}\\ =\sqrt{2+\sqrt{3}}.\sqrt{4-\left(2+\sqrt{3}\right)}\\ =\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}\\ =\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\\ =\sqrt{4-\sqrt{3^2}}\\ =\sqrt{4-3}\\ =\sqrt{1}\\ =1\)
6 tháng 11 2023
1: \(\left(\sqrt{10}-\sqrt{14}\right)\cdot\sqrt{6+\sqrt{35}}\)
\(=\left(\sqrt{5}-\sqrt{7}\right)\cdot\sqrt{12+2\sqrt{35}}\)
\(=\left(\sqrt{5}-\sqrt{7}\right)\left(\sqrt{5}+\sqrt{7}\right)\)
=5-7=-2
2: Sửa đề: \(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2+\sqrt{2}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2}}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{2^2-\left(2+\sqrt{2}\right)}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2-\sqrt{2}}\)
\(=\sqrt{2\left(2+\sqrt{2}\right)\left(2-\sqrt{2}\right)}=\sqrt{2}\)
WR
4 tháng 7 2017
Sửa lại!
\(A=\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{3}}}}.\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{3}}}}..\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{4-2-\sqrt{2+\sqrt{3}}}.\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{2+\sqrt{2+\sqrt{3}}}.\sqrt{2-\sqrt{2+\sqrt{3}}}.\)
\(=\sqrt{2+\sqrt{3}}.\sqrt{4-2-\sqrt{3}}=\sqrt{2+\sqrt{3}}.\sqrt{2-\sqrt{3}}=\sqrt{4-3}=1.\)
30 tháng 7 2023
1:
\(A=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2^2-\left(2+\sqrt{2-\sqrt{3}}\right)}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{2-\sqrt{3}}}\cdot\sqrt{2-\sqrt{2-\sqrt{3}}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{4-2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
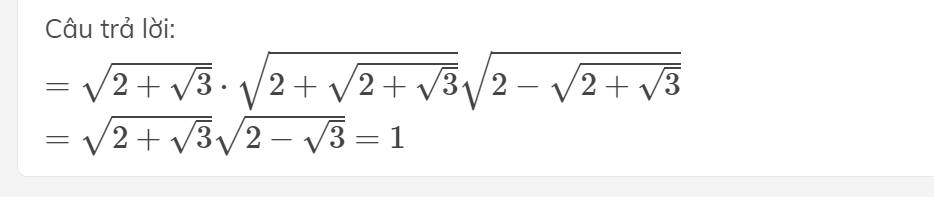
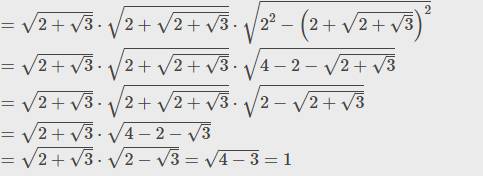
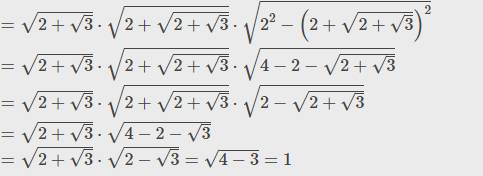
Chắc cái căn ở số 2 thứ 4 phải bao trùm luôn chứ nhỉ? nếu ko nó sẽ ko tồn tại quy luật dẫn tới ... ở đằng sau
Đặt \(x=\sqrt{2+\sqrt{2+\sqrt{2+...}}}>0\)
\(\Rightarrow x^2=2+\sqrt{2+\sqrt{2+\sqrt{2+...}}}\)
\(\Rightarrow x^2=2+x\)
\(\Rightarrow x^2-x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1< 0\left(ktm\right)\\x=2\end{matrix}\right.\)
Vậy \(x=2\)