có mấy cách chứng minh tia phân giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Tia phân giác của một góc là tia nằm giữa hai cạnhcủa góc và tạo với hai cạnh ấy hai góc bằng nhau. 1. Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
- trên cùng một nủa mặt phẳng bờ chứa tia Ox có ^xOy<^xOz thì tia Oy nằm giữa tia Ox và Oz
- Nếu tia Ox và Oy nằm trên hai nửa mặt phẳng đối nhau bờ chứa tia Oz thì tia Oz nằm giữa tia Ox và Oy

Chứng minh:
-Tia đó đi qua 1 đỉnh và tâm đường tròn ngoại tiếp
-2 góc tạo bởi tia đó với 2 cạnh kề bằng nhau
-Khoảng cách từ 1 điểm bất kì thuộc tia đến 2 cạnh kề tia đó bằng nhau
-Tia đó chia cạnh đối diện thành 2 cạnh a',b'; 2 cạnh kề tương ứng có độ dài a,b
\(\frac{a'}{b'}=\frac{a}{b}\)
Nhiều cách nữa nhưng mik chia nghĩ ra
Để chứng minh tia Oz là tia phân giác của góc xÔy
1. Chứng minh tia Oz nằm giữa tia Ox, Oy và
2. Chứng minh hay
3. Chứng minh trên tia Oz có một điểm cách đều hai tia Ox và Oy.
4. Sử dụng tính chất đường cao, trung tuyến ứng với cạnh đáy của tam giác cân.
5. Sử dụng tính chất đồng qui của ba đường phân giác.
6. Sử dụng tính chất đường chéo của hình thoi, hình vuông.
7. Sử dụng tính chất hai tiếp tuyến giao nhau trong đường tròn.
8. Sử dụng tính chất tâm đường tròn nội tiếp tam giác.

Hình tự vẽ, Giải :
Kẻ tia phân giác góc A => góc A1 = góc A2.
Tia phân giác góc A cắt BC tại M
Tự các dữ kiện suy ra tam giác ABM = tam giác ACM ( c.c.c )
Suy ra góc B = góc C ( tương ứng )

Chứng minh Oz là tia phân giác của góc xÔy.
1. C/minh tia Oz nằm giữa tia Ox, Oy và xÔz = yÔz hay xÔz = xÔy.
2. Chứng minh trên tia Oz có một điểm cách đều hai tia Ox và Oy.
3. Sử dụng tính chất đường cao, trung tuyến ứng với cạnh đáy của cân.
4. Sử dụng tính chất đồng qui của ba đường phân giác.
5. Sử dụng tính chất đường chéo của hình thoi, hình vuông.
6. Sử dụng tính chất hai tiếp tuyến giao nhau trong đường tròn.
7. Sử dụng tính chất tâm đường tròn nội tiếp tam giác.

Chứng minh Tia Oz là tia phân giác của góc xOy có 2 cách :
C1: xOz = yOz và Oz nằm giữa hai tia Õ và Oy
C2 : xOz = yOz = \(\frac{xOy}{2}\)

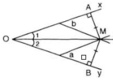
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.

\(\left\{{}\begin{matrix}AB=AC\\BD=DC\\AD\text{ chung}\end{matrix}\right.\Rightarrow\Delta ADB=\Delta ADC\left(c.c.c\right)\\ \Rightarrow\widehat{BAD}=\widehat{CAD}\)
Vậy AD là p/g \(\widehat{BAC}\)

mình nghĩ đề b có vấn đề CK là tia p/g cũa góc ACK.
C A B D E K M G I F N P
a, Vì \(\widehat{BAC}=120^o\) và AD là phân giác \(\widehat{BAC}\) nên \(\widehat{BAD}=\widehat{DAC}=\widehat{CAK}=60^o\)
Do đó: AC là phân giác \(\widehat{DAK}\)
Lấy M,N,P lần lượt là chân đường vuông góc hạ từ I xuống BC, AD, BK
Ta có DI là phân giác \(\widehat{DAC}\) nên IM=IN
I thuộc AC là phân giác \(\widehat{DAK}\) nên IN=IP
Do đó: IP=IM
Suy ra I thuộc đường phân giác \(\widehat{ABC}\) hay BI là phân giác \(\widehat{BAC}\)
Ta có góc BAC=120=>KAI=180-120=60=>AC là phân giác góc DAK(góc DAC=60); ta lại có DK là phân giác góc D => AC cắt DK tại I thuộc phân giác góc ABC(tc phân giác ngoài của tam giác) ; b) không hiểu chắc sai đề phải là ACx chứ;trên Cx lấy E sao cho CE=CA gọiAE cắt CK tai M ; chứng minh tam giác CAM=CEM=> góc ACM=ECM=> CM là pg góc ACE hay AK là pg góc ACx
chỉ có một cách thôi bạn à!!! giả sử hình này nhé
x O y z
để chứng minh tia Oz là tia p/giác của \(\widehat{xOy}\)thì ta p chứng minh tia Oz nằm giữa hai tia Ox và Oy và chứng minh \(\widehat{yOz}=\widehat{zOy}\). chỉ cần thế thôi!!!