đề bài : với giá trị nào của x thì giá trị biểu thức x^2-8x+12 không âm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2023
\(x+\dfrac{1}{x-2}=\dfrac{x^2-2x+1}{x-2}=\dfrac{\left(x-1\right)^2}{x-2}\)
Để biểu thức trên không âm hay \(\dfrac{\left(x-1\right)^2}{x-2}\ge0\) thì:
\(\left[{}\begin{matrix}x-2>0\\\left(x-1\right)^2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x>2\\x=1\end{matrix}\right.\)
CM
7 tháng 3 2017
Giá trị của biểu thức 6 x + 1 18 + x + 3 12 không nhỏ hơn giá trị của biểu thức 5 x + 3 6 + 12 - 5 x 9 nghĩa là 6 x + 1 18 + x + 3 12 ≥ 5 x + 3 6 + 12 - 5 x 9
Ta có:
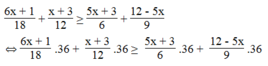
⇔ 12x + 2 + 3x + 9 ≥ 30x + 18 + 48 – 20x
⇔ 12x + 3x – 30x + 20x ≥ 18 + 48 – 2 – 9
⇔ 5x ≥ 55
⇔ x ≥ 11
Vậy với x ≥ 11 thì giá trị của biểu thức 6 x + 1 18 + x + 3 12 không nhỏ hơn giá trị của biểu thức 5 x + 3 6 + 12 - 5 x 9
11 tháng 12 2019
P = - x2 - 8x + 5
P = - ( x2 + 8x - 5 )
P = - ( x2 + 2 . 4 . x + 42 - 42 - 5 )
P = - [ ( x + 4 )2 - 21 ]
P = - ( x + 4 )2 + 21 \(\le\)21
Dấu " = " xảy ra \(\Leftrightarrow\)x + 4 = 0
\(\Rightarrow\)x = - 4
Vậy : Min P = 21 \(\Leftrightarrow\)x = - 4
CM
9 tháng 3 2018
Từ giả thiết suy ra (x + 1)2 - 4 ≤ (x - 3)2
Û x2 + 2x + 1 - 4 ≤ x2 - 6x + 9
Û x2 + 2x + 1 - 4 - x2 + 6x - 9 ≤ 0
Û 8x ≤ 12
Û x ≤ 3/2
Vậy x ≤ 3/2là giá trị cần tìm.
Đáp án cần chọn là: C
PK
0
Để x2 - 8x + 12 không âm thì x2 - 8x + 12 ≥ 0
<=> ( x - 2 )( x - 6 ) ≥ 0
Xét hai trường hợp :
1. \(\hept{\begin{cases}x-2\ge0\\x-6\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge2\\x\ge6\end{cases}}\Leftrightarrow x\ge6\)
2. \(\hept{\begin{cases}x-2\le0\\x-6\le0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\le2\\x\le6\end{cases}}\Leftrightarrow x\le2\)
Vậy với \(\orbr{\begin{cases}x\ge6\\x\le2\end{cases}}\)thì x2 - 8x + 12 không âm
Theo bài ra ta có : \(x^2-8x+12\ge0\)
\(\Leftrightarrow\left(x-6\right)\left(x-2\right)\ge0\)
TH1 : \(\hept{\begin{cases}x-6\ge0\\x-2\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge6\\x\ge2\end{cases}\Leftrightarrow}x\ge6}\)
TH2 : \(\hept{\begin{cases}x-6\le0\\x-2\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le6\\x\le2\end{cases}\Leftrightarrow x\le2}}\)
Vậy với giá trị \(x\le2;x\ge6\)thì biểu thức trên ko âm