tìm tất cả các số nguyên để \(\frac{15n+8}{3n+4}\)có giá trị nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 3 2019
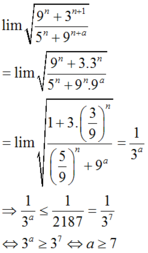
Kết hợp điều kiện đề bài
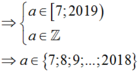
Vậy có 2018 - 7 + 1 = 2012 giá trị của a thỏa mãn.
Chọn C.
LT
1
27 tháng 7 2023
Để A là số nguyên thì 3n+5 chia hết cho n+4
=>3n+12-7 chia hết cho n+4
=>n+4 thuộc {1;-1;7;-7}
=>n thuộc {-3;-5;3;-11}
CL
2
TM
27 tháng 11 2016
\(A=2n:\frac{3n+1}{3}=2n.\frac{3}{3n+1}=\frac{6n}{3n+1}=\frac{6n+2-2}{3n+1}=\frac{2\left(3n+1\right)-2}{3n+1}\)
\(=\frac{2\left(3n+1\right)}{3n+1}-\frac{2}{3n+1}=2-\frac{2}{3n+1}\)
A nguyên <=> \(\frac{2}{3n+1}\) nguyên <=> 2 chia hết cho 3n+1
<=>\(3n+1\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
<=>\(3n\in\left\{-3;-2;0;1\right\}\)
<=>\(n\in\left\{-1;\frac{-2}{3};0;\frac{1}{3}\right\}\)
Vì n nguyên nên \(n\in\left\{-1;0\right\}\)
27 tháng 11 2016
A=\(=\frac{2n.3}{3n+1}=\frac{2.3n+2-2}{3n+1}=2-\frac{2}{3n+1}.\)
3n+1=+-1,+-2
n=0
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1
\(A=\dfrac{3n+1}{n-2}=\dfrac{3n-6+7}{n-2}=\dfrac{3\left(n-2\right)+7}{n-2}=3+\dfrac{7}{n-2}\)
A nguyên \(\Rightarrow\dfrac{7}{n-2}\) nguyên
\(\Rightarrow n-2=Ư\left(7\right)\)
\(\Rightarrow n-2=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow n=\left\{-5;1;3;9\right\}\)
JK
24 tháng 7 2019
\(B=\frac{6n-5}{3n+1}\inℤ\)
=> 6n - 5 ⋮ 3n + 1
=> 6n + 2 - 7 ⋮ 3n + 1
=> 3(3n + 1) - 7 ⋮ 3n + 1
=> 7 ⋮ 3n + 1
=> 3n + 1 thuộc Ư(7)
=> 3n + 1 thuộc {-1; 1; -7; 7}
=> 3n thuộc {-2; 0; -8; 6}
=> n thuộc {0; 2} vì n thuộc Z
XO
24 tháng 7 2019
a) Để \(B\inℤ\)
\(\Rightarrow\left(6n-5\right)⋮\left(3n+1\right)\)
\(\Rightarrow\left(6n+2-7\right)⋮\left(3n+1\right)\)
\(\Rightarrow2.\left(3n+1\right)-7⋮\left(3n+1\right)\)
Vì \(2.\left(3n+1\right)⋮\left(3n+1\right)\)
nên \(-7⋮3n+1\)
\(\Rightarrow3n+1\inƯ_{\left(-7\right)}\)
\(\Rightarrow3n+1\in\left\{1;-1;7;-7\right\}\)
Lập bảng xét 4 trường hợp ta có :
| \(3n+1\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(n\) | \(0\) | \(-\frac{2}{3}\) | \(2\) | \(-\frac{8}{3}\) |
Vậy \(n\in\left\{0;2\right\}\)
NN
1
11 tháng 3 2016
Mình sẽ làm chi tiết như sau nếu bạn ko hiểu thì tùy
\(C=\frac{6n-1}{3n+2}=\frac{\left(6n+4\right)-5}{3n+2}\)
Để C là số nguyên thì \(3n+2\inƯ\left(-5\right)\)
\(\Rightarrow3n+2=-5;3n+2=5;3n+2=1;3n+2=-1\)
Giải từng trường hợp ra thì sẽ có n thôi nhé
11 tháng 8 2016
mk giải câu a thui nha
để \(\frac{6n-1}{3n+2}\)là số nguyên thì:
(6n-1) sẽ phải chia hết cho(3n+2)
mà (3n+2) chja hết cho (3n+2)
=> 2(3n+2) cx sẽ chia hết cho (3n+2)
<=> (6n+4) chia hết cho (3n+2)
mà (6n-1) chia hết cho (3n+2)
=> [(6n+4)-(6n-1)] chja hết cho (3n+2)
(6n+4-6n+1) chja hết cho 3n+2
5 chia hết cho3n+2
=> 3n+2 \(\in\){1,5,-1,-5}
ta có bảng
3n+2 | 1 | 5 | -1 | -5 |
3n | 3 | 7 | 1 | -3 |
| n | 1 | -1 |
vậy....
22 tháng 3 2016
bạn có thể giải thích ra được không !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
n=0 nhé
Ta có : \(\frac{15n+8}{3n+4}=\frac{5\left(3n+4\right)-12}{3n+4}=5-\frac{12}{3n+3}\)
Để phân số trên có giái trị nhỏ nhất => \(\frac{12}{3n+4}\) lớn nhất
=> 3n+4 nhỏ nhất
xét : 3n+4 là số nguyên âm mà không có số nguyên âm nhỏ nhất => loại
xét : 3n+4 là số nguyên dương
=> 3n+4 = 1
=> 3n=-3
=> n= -1
Vậy để phân số trên có giái trị nhỏ nhất thì n = -1