Cho p = x3 – 3x2 +5x, q = y3 – 3y2 +5y. Biết p + q=6. Hãy tính x+y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(P=3\left(x^2+2xy+y^2\right)-2\left(x+y\right)-100\)
\(P=3\left(x+y\right)^2-2.5-100\)
\(P=3.5^2-110\)
\(P=-35\)
b) \(Q=\left[x^3+y^3+3xy\left(x+y\right)\right]-2\left(x^2+2xy+y^2\right)+3.5+10\)
\(Q=\left(x+y\right)^3-2\left(x+y\right)^2+25\)
\(Q=5^3-2.5^2+25\)
\(Q=100\)

Có hai cách trình bày với bài này: một là bạn có thể liệt kê hết các phần tử ra hoặc bạn sắp xếp theo cùng thứ tự và tính như sau:


a) 10x(x-y) - 6y(y-x)
= 10x(x-y) +6y ( x-y)
=(10x+6y) (x-y)
b) 3x2 + 5y - 3xy -5x
= 3x(x-y) + 5(y-x)
= 3x(x-y) -5(x-y)
= (3x-5) ( x-y)
c) 3y2 - 3z2 +3x2 + 6xy
=3(y2 - z2 + x2 + 2xy)
=3[(x2 +2xy+y2)-z2 ]
=3[(x+y)2 - z2 ]
=3(x+y-z) (x+y+z)
d) 16x3 + 54y3
=2(8x3 + 27y3 )
=2[(2x)3 + (3y)3 ]
=2(2x+3y) (4x2 - 6xy + 9y2 )
e) x2 - 25 -2xy+y2
=(x2-2xy+y2)-25
=(x-y)2 -52
=(x-y-5) (x-y+5)
f) (mình chưa làm ra )
{mong m.n bổ sung thêm..}
mấy câu trên bạn kia đã trả lời rồi nên mk k làm lại nx
f, x5 - 3x4 + 3x3 - x2
= x2 (x3 - 3x2 + 3x -1)
= x2 (x - 1)3
Chúc bạn học tốt!

a) P(x)+Q(x)=x3+3x2+3x-2-x3-x2-5x+2
=\(2x^2-2x\)
b)P(x)-Q(x)=(x3+3x2+3x-2)-(-x3-x2-5x+2)
=x3+3x2+3x-2+x\(^3\)+x\(^2\)+5x-2
=\(2x^3+4x^2+8x-4\)
c) Ta có H(x)=0
\(\Rightarrow\)\(2x^2-2x\)=0
\(\Rightarrow\)2x(x-1)=0
\(\Rightarrow\left[{}\begin{matrix}2x=0\\x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy nghiệm của đa thức H(x) là 0;1
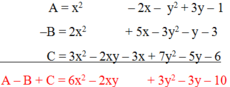
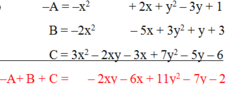
\(P+Q=6\Leftrightarrow x^3-3x^2+5x+y^3-3y^2+5y=6\Leftrightarrow\left(x^3-3x^2+3x-1\right)+\left(y^3-3y^2+3y-1\right)+\left(2x-4+2y\right)=0\)
\(\Leftrightarrow\left(x-1\right)^3+\left(y-1\right)^3+2\left(x+y-2\right)=0\Leftrightarrow\left(x-1+y-1\right)\left[\left(x-1\right)^2-\left(x-1\right)\left(y-1\right)+\left(y-1\right)^2\right]+2\left(x+y-2\right)=0\)
\(\left[\left(x-1\right)^2-\left(x-1\right)\left(y-1\right)+\left(y-1\right)^2+2\right]\left(x+y-2\right)=0\)
=> x+y-2=0 <=> x+y=2
( trong ngoặc là bình phương thiếu của hiệu. có dạng \(a^2-ab+b^2\) luôn >=0 => +2 vào thì luôn khác 0