cho tứ giác ABCD. chứng minh rằng ; CV(ABCD) < 2(AC+BD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KK
30 tháng 8 2021
a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân
PT
1
NH
1
27 tháng 8 2016
Ta có : góc A= góc B
Và góc C = góc D
Suy ra rằng 2 cặp đáy bằng nhau .
Nên : đpcm
BK
3 tháng 7 2021
ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang
Học tốt
DD
Đoàn Đức Hà
Giáo viên
3 tháng 7 2021
\(DB\)là phân giác \(\widehat{ADC}\)suy ra \(\widehat{ADB}=\widehat{CDB}\)(1)
\(BC=CD\)suy ra \(\Delta CBD\)cân tại \(C\)suy ra \(\widehat{CBD}=\widehat{CDB}\)(2)
(1)(2) suy ra \(\widehat{ADB}=\widehat{CBD}\)
mà hai góc này ở vị trí so le trong suy ra \(BC//AD\).
Suy ra \(ABCD\)là hình thang.
NB
0
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
T
1
17 tháng 9 2021
Xét ΔADC có DA=DC
nên ΔADC cân tại D
Suy ra: \(\widehat{DAC}=\widehat{DCA}\)
mà \(\widehat{DAC}=\widehat{BAC}\)
nên \(\widehat{BAC}=\widehat{ADC}\)
hay AB//CD
Xét tứ giác ABCD có AB//CD
nên ABCD là hình thang
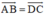
Dựa vào BĐT tam giác ta có:
AO+OB>AB
OB+OC>BC
OC+OD>CD
OD+OA>AD
=>OA+OB+OB+OC+OC+OD+OD+OA>AB+BC+CD+DA
=>2(AC+BD)>AB+BC+CD+DA(ĐPCM)