1)Chứng tỏ rằng:
a) a+b /a+b+c+d+e+g < 1/3
b)a+c+e / a+b+c+d+e+g < 1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 5 2022
a: Ta có: ΔDEF cân tại D
mà DK là đường trung tuyến
nên DK là đường cao
c: Xét ΔBFK vuông tại K có BF là cạnh huyền
nên FK<FB(1)
Xét ΔDBF có \(\widehat{DBF}>90^0\)
nên FB<FD(2)
Từ (1) và (2) suy ra FK<FB<FD
27 tháng 3 2023
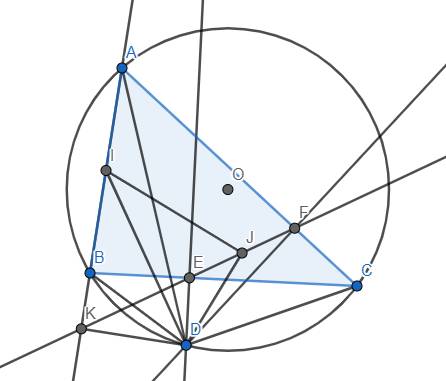
a) Theo đề bài, ta có \(\widehat{DEC}=\widehat{DFC}=90^o\) \(\Rightarrow\) Tứ giác CDEF nội tiếp do có 2 đỉnh kề nhau E, F cùng nhìn cạnh CD dưới góc vuông. \(\Rightarrow\widehat{DFE}=\widehat{DCE}=\widehat{DCB}=\widehat{DAB}\) (do tứ giác ABDC nội tiếp nên \(\widehat{DCB}=\widehat{DAB}\)). Từ đó suy ra đpcm.
b) Có \(\widehat{KBD}=\widehat{ACD}\) (do tứ giác ABDC nội tiếp) và \(\widehat{ACD}=\widehat{KED}\) (do tứ giác CDEF nội tiếp) \(\Rightarrow\widehat{KBD}=\widehat{KED}\) \(\Rightarrow\) Tứ giác DKBE nội tiếp.
Mặt khác, \(\widehat{BDA}=\widehat{BCA}=\widehat{EDF}\) và \(\widehat{BAD}=\widehat{BCD}=\widehat{EFD}\)
\(\Rightarrow\Delta DBA~\Delta DEF\left(g.g\right)\)\(\Rightarrow\dfrac{DA}{DF}=\dfrac{DB}{DE}\) \(\Rightarrow DA.DE=DB.DF\)
c) \(\Delta DBA~\Delta DEF\Rightarrow\dfrac{DB}{DE}=\dfrac{AB}{EF}=\dfrac{2BI}{2EJ}=\dfrac{BI}{EJ}\) . Lại có \(\widehat{DBI}=\widehat{DEJ}\) nên \(\Delta DBI~\Delta DEJ\left(c.g.c\right)\) \(\Rightarrow\widehat{DIB}=\widehat{DJE}\) hay \(\widehat{DIK}=\widehat{DJK}\) \(\Rightarrow\) Tứ giác DJIK nội tiếp \(\Rightarrow\) \(\widehat{DJI}=180^o-\widehat{DKI}\) . Lại có \(\widehat{DKI}=180^o-\widehat{BED}=90^o\) (do tứ giác DKBE nội tiếp) \(\Rightarrow\widehat{DJI}=90^o\) \(\Rightarrow\) đpcm