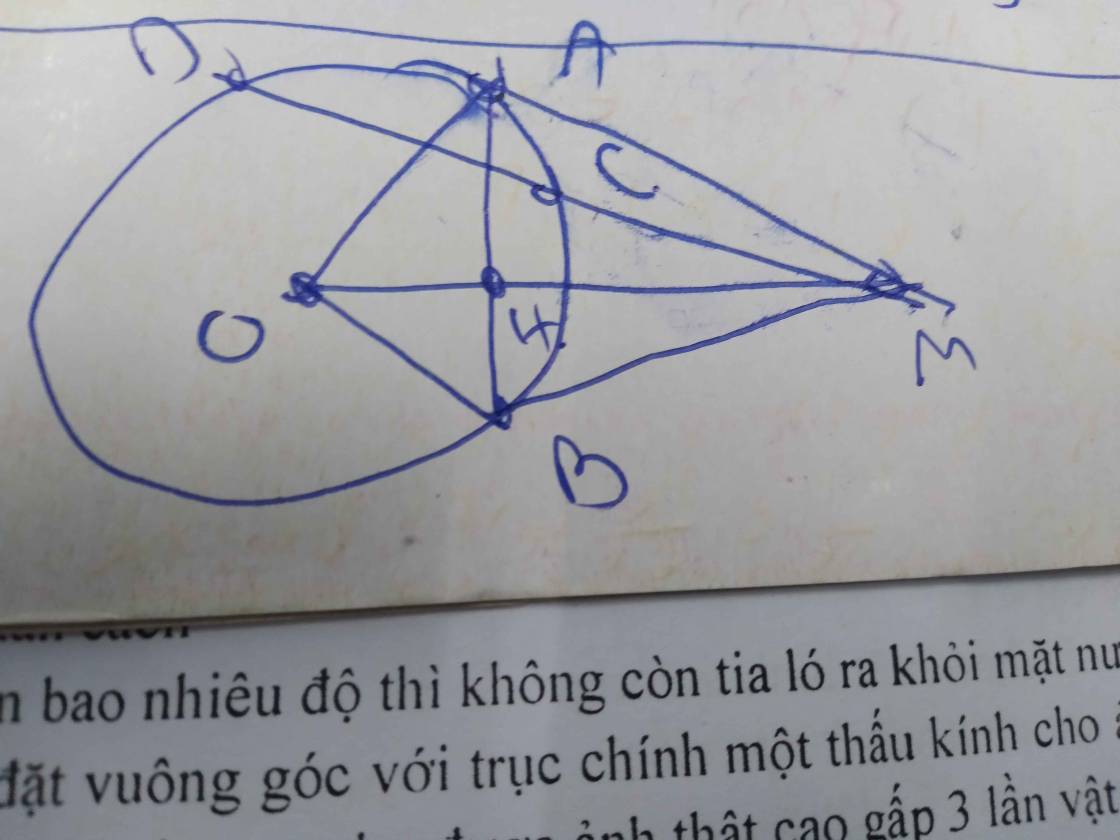
cho đường tròn (O) và điểm M nằm ngoài (O). Từ điểm M kẻ hai tiếp tuyến MA,MC (A,C là các tiếp điểm ) tới đường tròn(O) .Từ điểm M kẻ cát tuyến MBD (B nằm giữa M và D, MBD ko đi qua O). gọi H là giao điểm của OM và AC . từ C kẻ đường thẳng song song với BD cắt đường tròn(O) tại E (E khác C) , gọi K là giao điểm của AE và BD . chứng minh
a, Tứ giác OAMC nội tiếp
b, K là trung điểm của BD
c, AC là phân giác của góc BHD