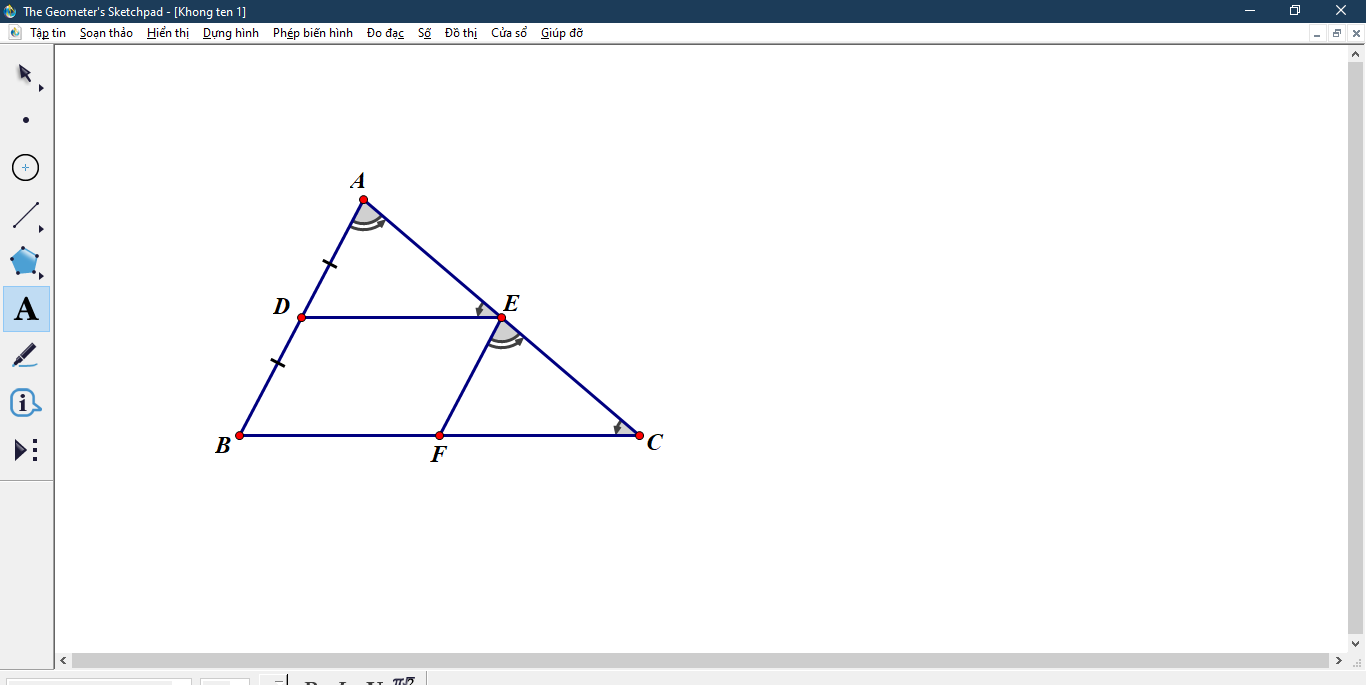
cho tam giác ABC.D là trung điểm của AB.E là tung điểm của AC.Đường thẳng qua E cắt BC ở F.CMR
a,AD=EF
b,tam giác ADE =tam giác EFC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 12 2021
a: Xét tứ giác BDEF có
DE//BF
BD//EF
Do đó: BDEF là hình bình hành
Suy ra: FE=BD
hay FE=AD
10 tháng 12 2021
c: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
25 tháng 12 2016
a)Nối D với F. Xét \(\Delta BDF\) và \(\Delta FDE\) ta có:
\(\widehat{BDF}=\widehat{DFE}\) (so le trong (Vì AB//EF (gt)))
DF cạnh chung
\(\widehat{DFB}=\widehat{FDE}\) (so le trong (Vì DE//BC (gt)))
\(\Rightarrow\Delta BDF\)\(=\Delta FDE\) (g.c.g)
\(\Rightarrow DB=EF\) (2 cạnh tương ứng )
Mà \(DB=DA\) (D là trung điểm AB)
Suy ra AD=EF
b)Xét \(\Delta ADE\) và \(\Delta EFC\:\) ta có:
\(\widehat{ADE}=\widehat{CFE}\) (\(=\widehat{BAC}\); đồng vị của DE//BC và EF//AB)
\(AD=EF\) (cmt)
\(\widehat{DAE}=\widehat{FEC}\) (đồng vị của DE//BC)
\(\Rightarrow\Delta ADE=\Delta EFC\) (g.c.g)
c)Vì \(\Delta ADE=\Delta EFC\) (cmt)
Suy ra \(AE=EC\) (2 cạnh tương ứng )
8 tháng 8 2021
Xét \(\Delta ABC\) có AD=DB;DE//BC nên AE=EC hay E là trung điểm AC
Xét \(\Delta ADE\) và \(\Delta EFC\) có:
\(\left\{{}\begin{matrix}\widehat{DAE}=\widehat{FEC}\\AE=EC\left(cmt\right)\\\widehat{AED}=\widehat{ECF}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ADE\) \(=\) \(\Delta EFC\)\(\left(g.c.g\right)\)
Tick hộ nha
8 tháng 8 2021
Vì AD=BD và d//BC
=> E là trung điểm của AC
=> AE = EC
Vì DE//BC
=> \(\widehat{AED}=\widehat{ECF}\) (2 góc đồng vị)
Vì ÈF//AB
\(\Rightarrow\widehat{DAE}=\widehat{FEC}\) (2 góc đồng vị)
Xét ΔADE và ΔECF có;
\(\widehat{AED}=\widehat{ECF}\) (cmt)
AE = EC
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=> ΔADE = ΔECF (g-c-g)
xet tam giac BDF va tam giac DEF ta co
DF=DF ( canh chung)
goc BDF = goc DFE ( 2 goc sole trong va BA//EF)
goc DFB = goc FDE ( 2 goc sole trong va DE//BC)
--> tam giac BDF = tam giac DEF ( g-c-g) --> BD= EF ( 2 goc tuong ung)
ma AD=BD ( D la trung diem AB) nen AD=EF
b)ta co
goc ADE=goc BAC ( 2 goc dong vi va DE//BC)
goc CEF = goc BAC ( 2 goc dong vu va EF//AB)
--> goc ADE = goc CFE
xet tam giac ADE va tam giac EFC ta co
goc ADE=goc CFE ( cmt
AD= EF ( cm a)
goc DAE = goc FEC ( 2 goc dong vi va DE//BC)
--> tam giac ADE = tam giac EFC ( c-g-c)