cho tam giác abc , m là trung điểm của cạnh bc . trên tia đối của tia ma lấy điểm e sao cho me=ma a) chứng minh ; tam giác abm=tam giác ecm b)chứng minh; ab//ce
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$

a: Xét tứ giác ACEB có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ACEB là hình bình hành
Suy ra: AC//BE

a, Xét tam giác ACM và tam giác EMB có:
AM=ME
GÓC CMA =GÓC BME(đối đỉnh)
CM=MB
=> TAM GIÁC ACM=EMB( C.G.C)

`a,`
Xét `\Delta AMC` và `\Delta EMB`:
\(\left\{{}\begin{matrix}\text{MB = MC (M là trung điểm của BC)}\\\widehat{\text{AMC}}=\widehat{\text{BME}}\left(\text{đối đỉnh}\right)\\\text{MA = ME (gt)}\end{matrix}\right.\)
`=> \Delta AMC = \Delta EMB (c-g-c)`
`b,`
Vì `\Delta AMC = \Delta EMB (a)`
`->` $\widehat {ACM} = \widehat {EBM} (\text {2 góc tương ứng})$
Mà `2` góc này nằm ở vị trí sole trong
`->` \(\text{AC // BE (tính chất 2 đường thẳng //)}\)
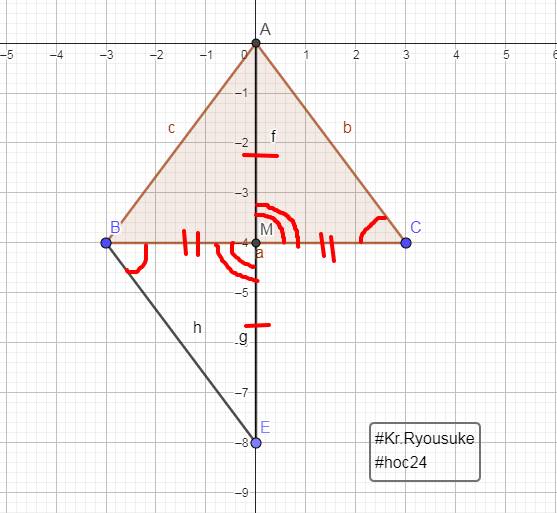

Hình vẽ mình họa
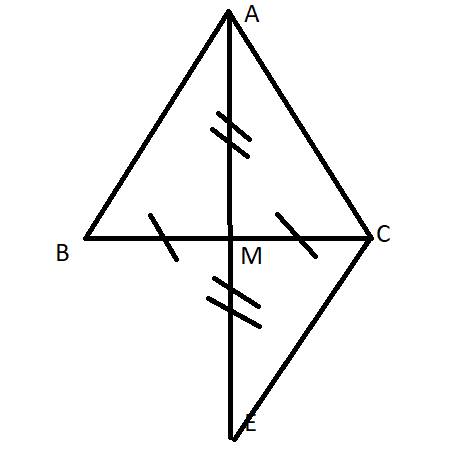
a, CM j cậu nhỉ .-.?
b, +)Xét ΔBAM và ΔCEM
AM=ME(GT)
BM=CM(M là trung điểm của BC)
\(\widehat{BMA}=\widehat{CME}\)(đối đỉnh)
=>ΔBAM=ΔCEM(c.g.c)
=>\(\widehat{BAE}=\widehat{AEC}\) (cạnh tương ứng)
+)\(\widehat{BAE}=\widehat{AEC}\) mà 2 góc này nằm ở vị trí so le trong
=>AB//CE

Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
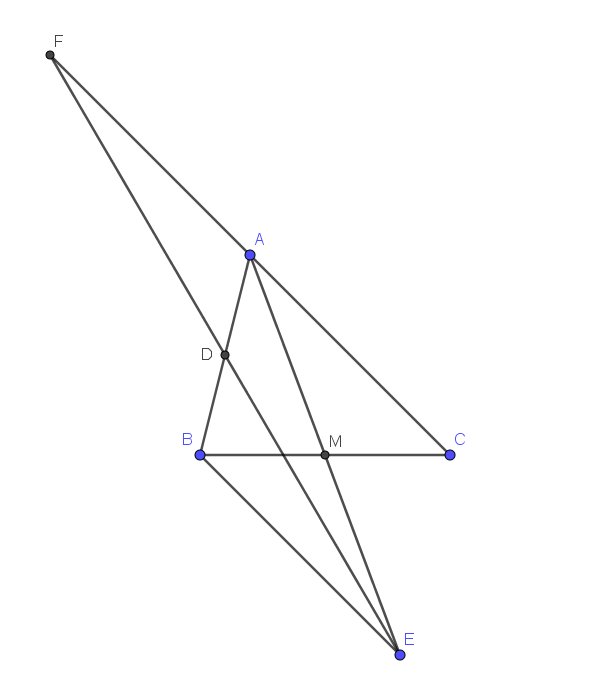
a) Xét tam giác ABM và tam giác ECM có:
MB = MC (vì M là trung điểm BC)
AM = EM (gt)
góc M1 = góc M2 (đối đỉnh)
=> Tam giác ABM = tam giác ECM (c.g.c)
b) Xét tứ giác ABCE có:
M là trung điểm BC (gt)
M là trung điểm AE (vì MA = ME)
=> tứ giác ABCE là hình bình hành
=> AB // CE (điều phải chứng minh)