Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình tự vẽ nha !
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
a) Xét ΔABM vàΔECM có:
AM= ME(giả thiết)
AMB=CME( đối đỉnh)
BM=MC( do M là trung điểm của BC)
=> ΔABM= ΔECM( c-g-c).
b) Do ΔABM =ΔECM( theo câu a)
nên BÂM= CÊM ( 2 góc tương ứng).
Mà 2 góc này ở vị trí so le trong nên AB//CE.

ddddddddddddddddddddddddddddddddddddddddddddddddddcccccccccccccccccccccccccccccccccccccc
Xét ABM và EMC có :
AM = ME
BM = CM
Góc AMB = góc CME ( đối đỉnh )
=> tam giac ABM = Tam giác EMC
Ta có : Tam giác AMB = tam giác EMC nên góc BAM = góc EMC
Mặt khác : 2 góc BAM và AEC nắm vị trí so le trong
=> AB // CE
c Xét tam giác AIB và tam gics CIK có :
AI = IC
BI = Ik
Góc AIB = góc CIK ( đối đỉnh )
=> tam giác AIB = tam giác CIK

Hình tự vẽ nha !
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
c/ d/ mình ko biết nha

Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.

a: Xét ΔMBA và ΔMCE có
MB=MC
góc BMA=góc CME
MA=ME
=>ΔMBA=ΔMCE
b: ΔMBA=ΔMCE
=>góc MBA=góc MCE
mà hai góc này so le trong
nên AB//CE
c: ΔMBA=ΔMCE
=>BA=CE
mà BA<CA
nên CE<CA
=>góc CAE<góc CEA
mà góc CEA=góc BAM
nên góc CAM<góc BAM
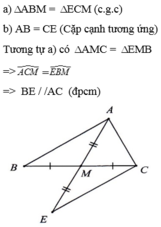
a) Xét tam giác ABM và tam giác ECM có:
MB = MC (vì M là trung điểm BC)
AM = EM (gt)
góc M1 = góc M2 (đối đỉnh)
=> Tam giác ABM = tam giác ECM (c.g.c)
b) Xét tứ giác ABCE có:
M là trung điểm BC (gt)
M là trung điểm AE (vì MA = ME)
=> tứ giác ABCE là hình bình hành
=> AB // CE (điều phải chứng minh)