Có bao nhiêu số nguyên dương n để 3 số 5; 12; n là độ dài 3 cạnh của một tam giác ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 3 2016
1, Để \(\frac{n+5}{n}\)là số nguyên<=>n+5 chia hết cho n<=>n chia hết cho n và 5 chia hết cho n<=>n thuộc ước của 5={-5;-1;1;5}<=> n=-5;-1;1;5
2,a:5 dư 1<=> a-1 chia hết cho 5 <=> a-1+45 chia hết cho 5 <=> a+44 chia hết cho5
a:7 dư 5 <=> a-5 chia hết cho 7 <=> a-5 +49 chia hết cho 7 <=> a+44 chia hết cho 7
=> a+44 thuộc BC(5;7)
<=> Ta có: 5=5
7=7
<=>BCNN(5;7)=5.7=35
<=>a+44=BC(5;7)=B(35)={70;105;140;175;....}
<=>a={26;61;96;131;.........}
3, gọi số cần tìm là x
<=> x=26.32=576
12 tháng 11 2021
ĐKXĐ: \(x\ne-1\)
\(X=\dfrac{2n+10}{n+1}=\dfrac{2\left(n+1\right)+8}{n+1}=2+\dfrac{8}{n+1}\in Z\)
\(\Rightarrow\left(n+1\right)\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
Kết hợp ĐKXĐ:
\(\Rightarrow n\in\left\{-9;-5;-3;-2;0;1;3;7\right\}\)
CM
31 tháng 3 2017
Chọn đáp án C.
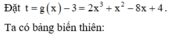
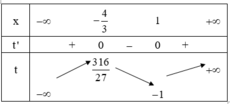
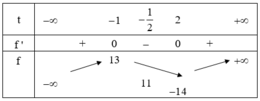
Do đó có 13 số nguyên dương m thỏa mãn yêu cầu bài toán.
DD
2
DD
Đoàn Đức Hà
Giáo viên
27 tháng 2 2021
\(A=\frac{n-3}{n-5}=\frac{n-5+2}{n-5}=1+\frac{2}{n-5}\)
\(A\)nguyên suy ra \(\frac{2}{n-5}\)nguyên suy ra \(n-5\inƯ\left(2\right)=\left\{-2,-1,1,2\right\}\)
\(\Rightarrow n\in\left\{3,4,6,7\right\}\).
11 tháng 7 2023
BCNN(50;8;20)=200
B(200)={0;200;400;600;800;1000;....}
Số nguyên dương có 3 chữ số là {200;400;600;800}
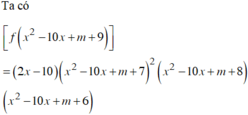
dựa theo bất đẳng thức của tg ta có ;tổng 2 cạnh bất kì của tg luôn lớn hơn cạnh còn lại của tg và hiệu của 2 cạnh bất kì của tg luôn bé hơn cạnh còn lại của tg
thế nên ;dựa theo bất đẳng thức của tm giác. trong tam giác này có '12+5 lớn hơn n ,n bé hơn 12-5
suy ra n lớn hơn 7 và bé hơn 17
mà n là số nguyên dương
nên n=8,9,10,......,16
vậy có tất cà 17 số nguyên dương n để 3 số 5;12;n là độ dai 3 cạnh của tam giác
chổ nào ko hiểu thì hỏi mình nha