Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ta có: ΔAMB=ΔDMC
nên AB=DC
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
c) Δ ABK = Δ ADK (câu b) => BK = DK (2 cạnh tương ứng)
và ABK = ADK (2 góc tương ứng)
Mà ABK + KBE = 180o (kề bù)
ADK + KDC = 180o (kề bù)
nên KBE = KDC
Xét Δ KBE và Δ KDC có:
BE = CD (gt)
KBE = KDC (cmt)
BK = DK (cmt)
Do đó, Δ KBE = Δ KDC (c.g.c)
=> BKE = DKC (2 góc tương ứng)
Lại có: BKD + DKC = 180o (kề bù)
Do đó, BKE + BKD = 180o
=> EKD = 180o
hay 3 điểm E, K, D thẳng hàng (đpcm)
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
XétΔCAD có
CM là đường cao
CM là đường trung tuyến
Do đó: ΔCAD cân tại C
Ta có: ΔCAD cân tại C
mà CM là đường cao
nên CM là phân giác của góc ACD
=>CB là phân giác của góc ACD
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ta có; ΔAMB=ΔDMC
=>AB=DC
Ta có: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét ΔNAB và ΔNCE có
NA=NC
\(\widehat{ANB}=\widehat{CNE}\)(hai góc đối đỉnh)
NB=NE
Do đó: ΔNAB=ΔNCE
=>AB=CE
Ta có: ΔNAB=ΔNCE
=>\(\widehat{NAB}=\widehat{NCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
Ta có: AB//CE
AB//CD
CE,CD có điểm chung là C
Do đó: E,C,D thẳng hàng
Ta có: EC=AB
CD=AB
Do đó: EC=CD
mà E,C,D thẳng hàng
nên C là trung điểm của ED
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD và AB=CD
b: Xét ΔABC và ΔCDA có
AB=CD
BC=DA
AC chung
Do đó: ΔABC=ΔCDA
Suy ra: \(\widehat{ABC}=\widehat{CDA}\)
Suy ra: BC=DA
hay BC=2AM
c: Xét tứ giác BDAE có
BD//AE
BD=AE
Do đó: BDAE là hình bình hành
Suy ra: BE//AM
d: Ta có: BDAE là hình bình hành
nên Hai đường chéo DE và BA cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AB
nên O là trung điểm của DE
hay D,O,E thẳng hàng
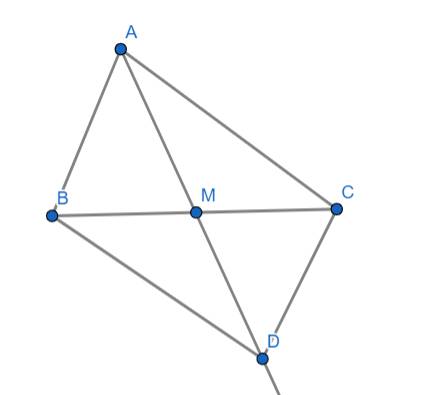
Youcho tam giác nhọn ABC, AB<AC. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD a) chứng minh tam giác AMB=tam giác DMC b) chứng minh AB=DC c)chứng minh AB song song với CD
a/ Xét tam giác AMB và tam giác DMC có:
MA= MD( GT)
AMB=CMD( 2 góc đối đỉnh)
MB= MC( M là trung điểm của BC)
=> tam giác AMB= tam giác DMC(c.g.c)
b/ => góc BAM=MDC( theo a)
=> AB// CD( 2 góc ở vị trí sole trong bằng nhau)
c/ Xét tam giác AEM và tam giác AFM có:
AE= EF(GT)
góc EAM= FDM( theo b)
AM= DM( GT)
=> tam giác AEM = tam giác AFM(c.g.c)
Do đó: góc AME= góc DMF
=>góc AME+ AMF= DMF+ AMF
=>EMF= 180 độ
Vậy => E, M, F thẳng hàng.
Xin lỗi ! Bạn có thể tự vẽ hình dc ko?