một ô tô khởi hành từ tỉnh a về tỉnh b với tốc độ 60km/h. sau đó trở về a với tốc độ 40km/h. biết a cách b là 120 km/h câu a : tính thời gian đi từ A đến B và B đến A câu b : tính tốc độ trung bình ô tô đi từ A đến B và từ B về A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài AB là x
Thời gian đi là x/40
Thời gian về là x/50
Theo đề, ta có: x/40+x/50=5,4
=>x=120

Đổi là \(30'=0,5h\)
a) Thời gian đi từ A -> B là:
\(t=S:V=100:50=2h\)
Quãng đường từ B -> C là:
\(S=t.V=0,5.40=20km\)
b) Vận tốc trung bình của xe đi từ A -> C là:
\(V_{tb}=\dfrac{S_{AB}+S_{BC}}{t_{AB}+t_{BC}}=\dfrac{100+20}{2+0,5}=48\) km/h

Gọi quãng đường AB là x ( x > 0 )
Theo bài ra ta có pt \(\frac{x}{45}+\frac{x}{60}=3+\frac{1}{2}=\frac{7}{2}\Rightarrow x=90\)(tm)
Vậy quãng đường ab DÀI 90 KM

Gọi quang duong AB là x (km, x>0)
Thời gian ô tô đi là x/50
Thoi gian o to ve là x/40
Vì t/gian về nhiều hơn t/gian đi là 30 phút(=1/2)nên ta có pt:
x/40-1/2=x/50
đến đây tự giải
đs:100

Vì cùng một quãng đường thì vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên tỉ số thời gian khi đi và thời gian khi về của ô tô là:
50 : 40 = \(\dfrac{5}{4}\)
Đổi 42 phút = \(\dfrac{7}{10}\)
Theo bài ra ta có sơ đồ
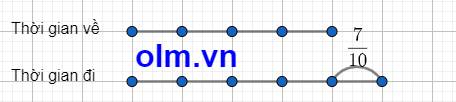
Theo sơ đồ ta có:
Thời gian đi là: \(\dfrac{7}{10}\): ( 5-4) \(\times\) 5 = \(\dfrac{7}{2}\)(giờ)
Quãng đường AB dài là: 40 \(\times\) \(\dfrac{7}{2}\) = 140 (km)
Đáp số: 140 km

gọi độ dài quãng đường AB là: x (đơn vị: km, x>0)
=> thời gian mà ô tô khởi hành là: `x/40` (giờ)
vận tốc ô tô về là: `40-10=30`(km/h)
`=>` thời gian mà ô tô về là `x/30` (giờ)
vì tổng thời gian cả đi lẫn về hết 7 giờ nên ta có phương trình sau
`x/40+x/30=7`
`<=>x(1/40+1/30)=7`
`<=>x*7/120=7`
`<=>x=120(tm)`
vậy độ dài quãng đường AB là: `120km`

Gọi độ dài quãng đường AB là x (km) (x > 0)
Thời gian đi từ A đến B là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian đi từ B về A là: \(\dfrac{x}{60}\left(h\right)\)
Theo đầu bài, ta có: \(\dfrac{x}{40}+\dfrac{x}{60}+2=6,5\)
\(\Leftrightarrow\dfrac{3x+2x}{120}=4,5\)
\(\Leftrightarrow5x=540\)
\(\Leftrightarrow x=108\left(tm\right)\)
Vậy...

4
Gọi vận tốc của tàu thủy khi nc yên lặng là x (km/h),(x>4)
=) vận tốc xuôi dòng là x+4 (km/h)
=) thời gian xuôi dòng là \(\frac{80}{x+4}\)h
=)vận tốc ngược dòng là x-4 (km/h)
=) thời gian xuôi dòng là \(\frac{80}{x-4}\)h
mà tổng thời gian cả đi lẫn về là 8h20p=\(\frac{25}{3}\)h
nên ta có phương trình \(\frac{80}{x+4}\)+\(\frac{80}{x-4}\)=\(\frac{25}{3}\)
=) 240.(x-4) +240.(x+4) = 25. (x-4)(x+4)
=) x1=20 (thỏa mãn)
x2=-0.8 (loại)
Vậy vận tốc của tàu thủy khi nước yên lặng là 20km/h
Gọi quãng đường của mỗi chặng là S (km)
Quãng đường AB = 3S.
Thời gian đi chặng thứ nhất là: t1 = S/v1 = S/72
Thời gian đi chặng thứ hai là: t2 = S/v2 = S/60
Thời gian đi chặng thứ ba là t3 = S/v3 = S/40
Theo giả thiết: t1+t2+t3=4 <=> S/72 + S/60 + S/40 = 4
<=> S(1/72 + 1/60 + 1/40) = 4
<=> S.1/18 = 4
<=> S= 4.18 = 72 (km)
Vậy quãng đường AB là: 3.S = 3.72 = 216 (km)


a. Thời gian từ A đến B:
\(t_1=\dfrac{s_1}{v_1}=\dfrac{120}{60}=2h\)
Thời gian từ B đến A:
\(t_2=\dfrac{s_2}{v_2}=\dfrac{120}{40}=3h\)
b. Vận tốc trung bình:
\(v_{tb}=\dfrac{2\cdot120}{2+3}=48\left(\dfrac{km}{h}\right)\)
Tóm tắt:
\(v_1=60km\)/h
\(v_2=40km\)/h
\(s=120km\)
a) \(t_1=...h?\)
\(t_2=...h?\)
b) \(v_{tb}\)= ... km/h?
Giải:
a) Áp dụng công thức: \(v=\dfrac{s}{t}\Rightarrow t=\dfrac{s}{v}\)
Thời gian ô tô đi từ tỉnh A về tỉnh B là:
\(t_1=\dfrac{s}{v_1}=\dfrac{120}{60}=2\left(h\right)\)
Thời gian ô tô đi từ tỉnh B về tỉnh A là:
\(t_2=\dfrac{s}{v_2}=\dfrac{120}{40}=3\left(h\right)\)
b) Tốc độ trung bình ô tô đi từ A về B và từ B về A là:
\(v_{tb}=\dfrac{2s}{t_1+t_2}=\dfrac{120\times2}{2+3}=\dfrac{240}{5}=48\) (km/h)