Cho tam giác ABC có CA=CB và B=50 độ. Tính số đo A và C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lí tổng 3 góc trong 1 tam giác ta có :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^O\)
hay \(90^o+50^o+\widehat{C}=180^o\)
\(\Rightarrow\widehat{C}=180^o-90^o-50^o=40^o\)
b) Xét \(\Delta ABCvà\Delta DECcó\)
AC = DC ( gt )
CB = CE ( gt )
\(\widehat{ECD}=\widehat{BCA}\) ( đối đỉnh )
\(\Rightarrow\Delta ABC=\Delta DEC\) ( c.g.c )
c) \(\Rightarrow\widehat{E}=\widehat{B}\) ( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//DE\)
câu d mik chịu nhe !!!

\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
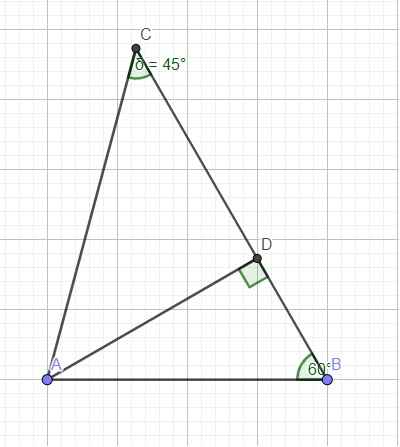
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
Xét tam giác ABC có CA = CB
=> Tam giác ABC cân tại C
=> Góc B = Góc A = 50 độ
Ta có: Góc B + Góc A + Góc C = 180 độ ( Tổng 3 góc trong 1 tam giác )
=> 50 + 50 + Góc C = 180
=> 100 + Góc C = 180
=> Góc C = 180 - 100 = 80 độ
Tam giác ABC có CA=CB
=> Tam giác ABC cân tại C
=>Góc A = Góc B = 50 độ (GT)
=>Góc C = 180 - A - B = 180 - 50 - 50 = 80