Lấy cạnh BC của một tam giác đều làm đường kính vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết BC = a, tính diện tích 2 đường viên phân ở ngoài tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 2 2019
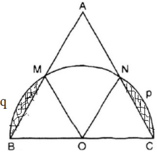
Gọi nửa đường tròn tâm O đường kính BC cắt hai cạnh AB và AC lần lượt tại M và N.
CM
26 tháng 9 2019
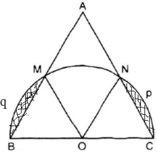
Gọi nửa đường tròn tâm O đường kính BC cắt hai cạnh AB và AC lần lượt tại M và N.
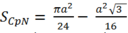
Vậy diện tích 2 viên phân bên ngoài tam giác là:
13 tháng 4 2017
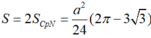
Lấy cạnh BC của một tam giác đều làm đường kính, vẽ một nửa đường tròn về cùng một phía với tam giác ấy đối với đường thẳng BC. Cho biết cạnh BC = a, hãy diện tích hình viên phân được tạo thành.
Hướng dẫn giải:
Gọi nửa đường tròn tâm O đường kính BC căt hai cạnh AB và AC lần lượt tại M và N.
∆ONC có OC = ON, = 60o nên ∆ONC là tam giác đều, do đó
= 60o.
Squạt NOC = =
.
S∆NOC = =
Diện tích hình viên phân:
SCpN = -
=
Vậy diện tích hình viên phhân bên ngoài tam giác là:
TA
22 tháng 3 2016
Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có
\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)
suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)
\(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)
\(=\overrightarrow{AC}\)
Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)
Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)
Do đó tứ giác EGFH là hình bình hành
22 tháng 2 2017
diện tích phần tam giác ngoài đường tròn là:
2x2x3,14=12,56
đáp số:12,56
22 tháng 2 2017
Diện tích phần tam giác nằm ngoài đường tròn là :
2 * 2 * 3,14 = 12,56
Đáp số : 12,56
bạn ơi k mình nha rồi mình sẽ kb với bạn
