Cho phương trình \(log_2^2x-2log_2x-4\sqrt{1-log_2x}=m\) với m là số thực .Số các giá trị nguyên thuộc đoạn [-2019;2019] của m để phương trình đã cho có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2021
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\7^x\ge m\end{matrix}\right.\)
\(\left[{}\begin{matrix}4log_2^2x+log_2x-5=0\\7^x-m=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x_1=2\\x_2=2^{-\dfrac{5}{4}}\\7^x=m\end{matrix}\right.\)
Với \(m\le0\) thì pt đã cho luôn có đúng 2 nghiệm
Vậy không cần xét tiếp, hiển nhiên là có vô số giá trị thực của m rồi?
5 tháng 2 2021
- Đặt \(a=x^2-2x\left(a\ge-1\right)\)
PTTT \(3\sqrt{a+3}=a+m\left(a\ge-m\right)\)
\(\Leftrightarrow9\left(a+3\right)=\left(a+m\right)^2=a^2+2am+m^2=9a+27\)
\(\Leftrightarrow a^2+a\left(2m-9\right)+m^2-27=0\)
Có : \(\Delta=\left(2m-9\right)^2-4\left(m^2-27\right)=4m^2-36m+81-4m^2+108\)
\(=-36m+189\)
- Để phương trình đề có 2 nghiệm phân biệt :
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(a_1+1\right)\left(a_2+1\right)>0\\a_1+1+a_2+1>0\end{matrix}\right.\)
Lại có : Theo vi ét : \(\left\{{}\begin{matrix}a_1+a_2=-2m+9\\a_1a_2=m^2-27\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\Delta>0\\a_1a_2+a_1+a_2+1>0\\a_1+a_2+2>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-36m+189>0\\m^2-27-2m+9+1=m^2-2m-17>0\\-2m+9+2=-2m+11>0\end{matrix}\right.\)
\(\Rightarrow m=\left(-\infty;1-3\sqrt{2}\right)\cup\left(1+3\sqrt{2};\dfrac{21}{4}\right)\) ( * )
- Có : \(x^2-2x=a\)
- Đặt \(f\left(x\right)=x^2-2x\)
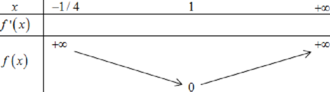
- Ta có đồ thị \(x^2-2x=0\)
- Từ độ thị hàm số : Để phương trình \(x^2-2x=a\) có 2 nghiệm phân biệt trong đoạn 0, 3 thì \(a=(-1;0]\)
Lại có : \(a=[-m;+\infty)\)
\(\Rightarrow-m\le0\)
\(\Rightarrow m\ge0\)
- Kết hợp với ( * )
\(\Rightarrow m\in\left(1+3\sqrt{2};\dfrac{21}{4}\right)\)
Vậy ...
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 6 2021
ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m
HP
14 tháng 4 2021
\(\sqrt{2x^2-8x+m}=x-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2-8x+m=\left(x-1\right)^2\\x-1\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+m-1=0\\x\ge1\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(x^2-6x+m-1=0\left(1\right)\) có nghiệm duy nhất thỏa mãn \(x\ge1\)
\(\left(1\right)\Leftrightarrow m=f\left(x\right)=-x^2+6x+1\)
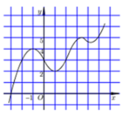
Đồ thi hàm số \(y=f\left(x\right)=-x^2+6x+1\):
Dựa vào đồ thị ta được \(m=10\)
P/s: Cái này t lười vẽ bảng biến thiên nên vẽ đồ thị đó, chứ bình thường viết trong vở thì dùng bảng biến thiên nhanh hơn nhiều.
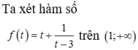
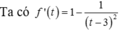
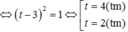
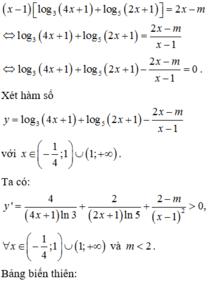
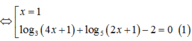
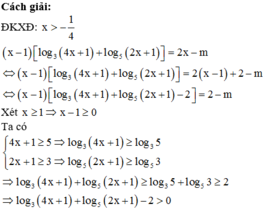
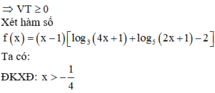
ĐKXĐ: \(0< x\le2\)
\(log_2x-2log_2x-4\sqrt{1-log_2x}=m\)
\(\Leftrightarrow\left(1-log_2x\right)^2-4\sqrt{1-log_2x}-1=m\)
Đặt \(\sqrt{1-log_2x}=t\ge0\)
\(\Rightarrow t^4-4t-1=m\)
Xét hàm \(f\left(t\right)=t^4-4t-1\) có \(f'\left(t\right)=4t^3-4=0\Rightarrow t=1\)
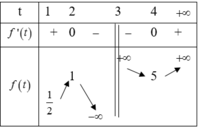
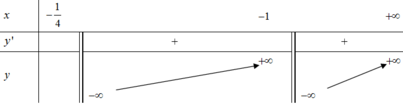
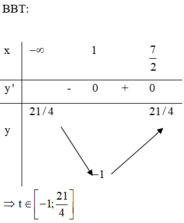
BBT:
Từ đó ta thấy \(f\left(t\right)=m\) có nghiệm khi \(m\ge-4\)
\(\Rightarrow\) Có 2024 giá trị nguyên của m thỏa mãn