Nêu vài cách xác định tâm của 1 đường tròn bất kì.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm

a: góc ACO=1/2*sđ cung AO=90 độ
=>OC//BD
Xét ΔADB có
O là trung điểm của AB
OC//BD
=>C là trung điểm của AD
b: BC là tiếp tuyến của (O')
=>góc BCO'=90 độ
=>góc O'CA=góc OCB
=>góc CO'O=góc O'CO=góc O'OC
=>ΔOO'C đều
=>C thuộc (O') sao cho ΔOCO' đều
=>Dựng đường trung trực của OO' cắt (O') tại C, ta đc điểm C cần tìm
Thế nào là đường tròn nội tiếp một tam giác? Nêu cách xác định tâm của đường tròn nội tiếp tam giác.

- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác.
- Tâm đường tròn nội tiếp tam giác là giao điểm của các tia phân giác của các góc trong của tam giác.

- Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác.
- Tâm đường tròn ngoại tiếp tam giác là giao điểm của các đường trung trực của các cạnh tam giác.

- Buộc dây vào một lỗ nhỏ A ở mép của vật rồi treo vật thẳng đứng. Khi vật nằm cân bằng, dùng bút đánh dấu phương của sợi dây AA' đi qua vật, trên vật. Tiếp theo, buộc dây vào một lỗ khác A, vào lỗ B chẳng hạn. Khi vật nằm cân bằng, đánh dâu phương sợi dây BB' qua vật.
- Giao điểm của hai đoạn thẳng đánh dấu trên vật AA' và BB' chính là trọng tâm G của vật.

Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực này cắt nhau tại O.
Khi đó; OA = OB = OC
Suy ra: O là tâm của đường viền.
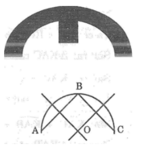
Lấy 3 điểm bất kì thuộc đường tròn đó, nối 3 điểm lại với nhau ta được 1 tam giác. Giao điểm 3 đường trung trực của tam giác chính là tâm đường tròn đó.
a) (x - 2)(x + 1) = 0\(\Rightarrow\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)
b) (x2 + 7)(x2 - 49) < 0
\(x^2\ge0\Rightarrow x^2+7>0\Rightarrow\hept{\begin{cases}x^2+7>0\\x^2-49< 0\end{cases}\Rightarrow-7< x^2< 49\Rightarrow x^2\in\left\{1;4;9;16;25;36\right\}}\)
\(\Rightarrow x\in\left\{-6;-5;-4;...;4;5;6\right\}\)
c) (x2 - 7)(x2 - 49) < 0 => x2 - 7 và x2 - 49 khác dấu mà x2 - 7 > x2 - 49
\(\Rightarrow x^2-7>0>x^2-49\Rightarrow7< x^2< 49\Rightarrow x^2\in\left\{9;16;25;36\right\}\Rightarrow x\in\left\{-6;-5;-4;-3;3;4;5;6\right\}\)